Основные определения, связь относительной и абсолютной производных

В ряде случаев приходится устанавливать соотношения между кинематическими характеристиками точки в двух различных системах отсчета, движущихся друг относительно друга.

Такова, например, задача об определении скорости и ускорения конца лопасти гребного винта в неподвижной системе отсчета через те же характеристики, но в системе отсчета, связанной с судном.

Будем называть сложным или абсолютным движением точки ее движение по отношению к неподвижной системе отсчета. Движение по отношению к подвижной системе отсчета будем называть относительным. Движение той точки подвижной системы отсчета, с которой в данный момент времени совпадает рассматриваемая точка, называется переносным движением.

Аналогичные названия имеют кинематические характеристики точки в указанных движениях.

Переносное и относительное движения предполагаются нами происходящими независимо, т.е. при рассмотрении картины переносного движения (КПД) относительное движение как бы «замораживается», а при рассмотрении картины относительного движения (КОД) «замораживается» переносное.

В зависимости от постановки задачи искомым может оказаться любое из трех названных движений.

Примечание. В силу произвольности выбора подвижной системы отсчета одно и то же абсолютное движение, в принципе, можно представить бесконечным множеством вариантов выделения составляющих движений; в каждом случае рациональный выбор варианта определяется реальной ситуацией.

Возьмем неподвижную координатную систему 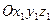и движущуюся по отношению к ней известным образом подвижную систему (рис.7.1).

Радиус-вектор точки М в координатной системе 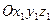(кинематическая характеристика абсолютного движения) обозначим 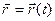, радиус-вектор точки А (начала подвижной системы отсчета) - .

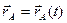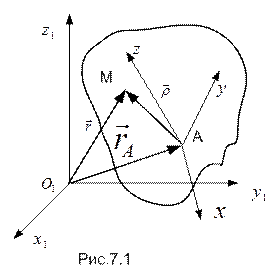
Положение точки М в подвижной координатной системе (кинематическая характеристика относительного движения) определяется вектором 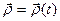, так что

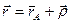. (7.1)

Особенность выражения (7.1) заключается в том, что входящие в него векторы задаются в различных системах отсчета. При проецировании (7.1) на оси любой системы отсчета следует учесть движение систем отсчета по отношению друг к другу.

Естественно, что дифференцирование векторных величин в подвижных системах отсчета обладает некоторыми особенностями вследствие переменности направлений ортов координатных осей.

Возьмем радиус-вектор точки 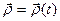, заданный в подвижной координатной системе проекциями 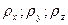. Обозначим орты подвижной системы соответственно 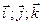. Тогда 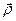может быть представлен в виде .

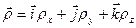Вследствие того, что оси подвижной координатной системы меняют свое направление, производная по времени о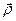т будет

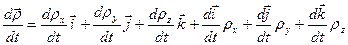. (7.2)

Сумма первых трех слагаемых представляет собой производную в подвижной системе осей и называется относительной или локальной производной (обозначим ее 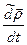), т.е.

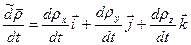. (7.3)

Ее физический смысл – скорость точки в подвижной системе отсчета, т.е. относительная скорость. Для того, чтобы выяснить смысл трех последних слагаемых в (7.2), вспомним, что в главе 4 была получена формула

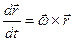, если 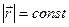. (7.4)

где 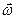- угловая скорость подвижной координатной системы.

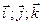Заменяя в этой формуле радиус-вектор последовательно на , получим

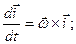
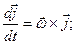
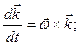(7.5)

С учетом сказанного сумма последних трех слагаемых в выражении (7.2) примет вид

.

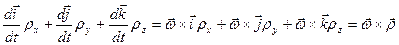(7.6)

Итак, абсолютная производная радиуса-вектора равна сумме его относительной производной и векторного произведения угловой скорости подвижной системы на этот радиус-вектор, т.е.

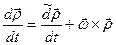. (7.7)

Date: 2015-09-03; view: 421; Нарушение авторских прав