Локальные кинематические характеристики и некоторые способы их определения

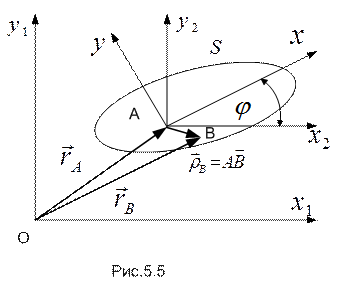
Пусть для плоской фигуры 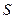известны уравнения движения (5.1). Найдем скорость и ускорение произвольной точки фигуры (рис.5.5).

Радиус-вектор 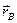, определяющий положение точки в неподвижной системе отсчета, может быть представлен в виде

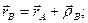
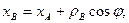
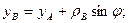(5.4)

где 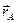- радиус-вектор точки 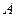в неподвижной системе отсчета, а 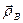- радиус-вектор точки в координатной системе 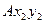(для недеформируемого тела ).

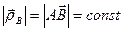Продифференцируем выражение (5.4) по времени:

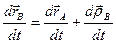. (5.5)

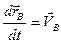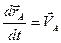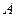Здесь и - скорости точек и в неподвижной системе отсчета. Слагаемое

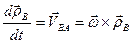(5.6)

есть скорость точки в полусвязанной системе 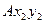, т.е. скорость, обусловленная вращением плоской фигуры вокруг полюса. Поэтому выражение для скорости точки примет вид

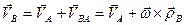, (5.7)

т.е. скорость произвольной точки плоской фигуры равна сумме скорости полюса 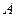и скорости точки при вращении плоской фигуры вокруг полюса .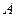

Графическая интерпретация формулы (5.7) приведена на рис.5.6.

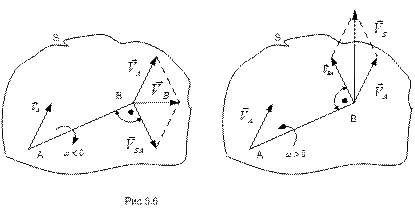
Модули и направления векторов, входящих в формулу (5.7), определяются из уравнений (5.2) и (5.6). При этом

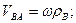
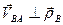. (5.8)

Для определения ускорения точки продифференцируем равенство (5.5) по времени:

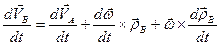. (5.9)

Здесь 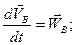- ускорения точек и 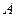в неподвижной системе отсчета; 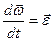- вектор углового ускорения; .

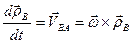Таким образом, ускорения точек и 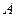связаны между собой соотношением

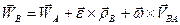. (5.10)

Второе и третье слагаемые являются соответственно вращательной (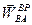) и осестремительной (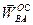) составляющими ускорения точки при вращении плоской фигуры вокруг полюса (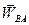) (см. рис.5.4.б). Тогда формулу (5.10) можно записать так

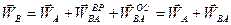. (5.11)

Графическая интерпретация формулы (5.11) при совпадающих по направлению векторах 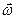и 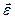приводятся на рис.5.7.

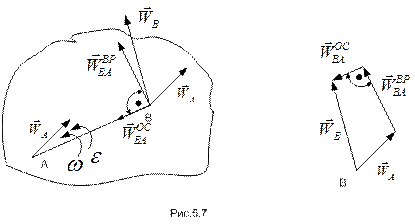
Ускорение 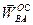направлено от рассматриваемой точки к полюсу, а ускорение 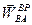- по перпендикуляру к отрезку АВ. Для определения модуля и направления ускорения точки следует воспользоваться уравнениями (5.3) и (5.10). При этом

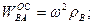
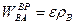. (5.12)

В некоторых случаях удобно использовать следующее полезное свойство: проекции скоростей точек твердого тела на прямую, проходящую через эти точки, равны между собой.

Для доказательства спроецируем (5.7) на прямую, проходящую через точки и 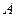. Очевидно, что проекция на эту прямую скорости 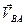равна нулю, т.к. 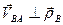. Тогда

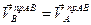. (5.13)

Отмеченное свойство справедливо и в общем случае движения твердого тела, так как является следствием неизменности расстояния АВ.

В том случае, когда за полюс выбрана точка , скорость которой равна нулю (рис.5.8), выражение (5.7) приобретает наиболее простой и удобный для расчета вид:

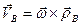. (5.14)

Это означает, что скорости точек при плоскопараллельном движении тела можно определять так же, как и в случае вращения тела вокруг неподвижной оси (см. параграф 3.2.2). При этом ось вращения движется; в каждый момент времени она перпендикулярна плоскости фигуры 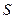и проходит через точку . Она называется мгновенной осью вращения тела, а точка - мгновенным центром скоростей (м.ц.с.) плоской фигуры. Часто мгновенная ось вращения – вне тела.

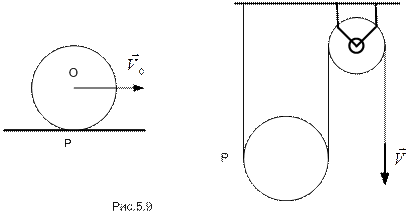
В некоторых случаях (рис.5.9) существование и положение такой точки очевидно. Так, если колесо катится без скольжения по рельсу, то равна нулю скорость той точки колеса, которая соприкасается с рельсом.

При плоском движении м.ц.с. существует всегда, за исключением случая, когда и, значит, скорости всех точек тела равны и параллельны (рис.5.10).

Существует и иная трактовка, утверждающая, что м.ц.с. существует и в этом случае, но располагается в бесконечности.

Очевидно, что если при этом равны ускорения всех точек, то движение тела поступательное, плоское. При неравных ускорениях движение называется мгновенно-поступательным.

Так движутся точки шатуна АВ кривошипно-шатунного механизма (рис.5.10), обладая в рассматриваемом положении равными скоростями, но разными ускорениями.

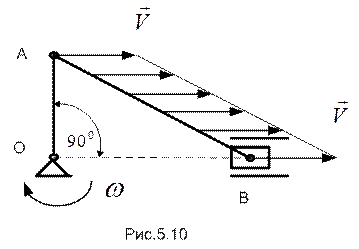
При возможны различные ситуации. В том случае, когда известны линии возможных направлений скоростей любых двух точек А и В плоской фигуры, м.ц.с. расположен на пересечении перпендикуляров к указанным линиям, восстановленным из этих точек (рис.5.11).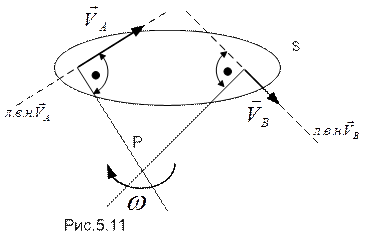

Если перпендикуляры параллельны, то движение плоской фигуры мгновенно-поступательное либо поступательное, плоское. Если перпендикуляры совпадают, то для определения положения м.ц.с. необходимо знать дополнительно модули скоростей точек 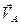и .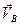

Тогда, используя формулу (5.6) и свойство пропорции, имеем:

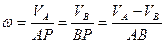. (5.15)

Соотношение (5.15) позволяет найти как длину любого из отрезков 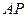или 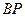, так и угловую скорость вращения тела.

ПРИМЕР 5.1. Судно на регулярном волнении совершает поперечную качку, причем угол крена судна изменяется по закону

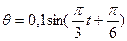, а центр тяжести судна G движется согласно уравнениям ; 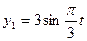. При 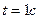определить скорость и ускорение вершины мачты А, которая расположена над центром тяжести судна на высоте 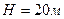(рис.5.12).

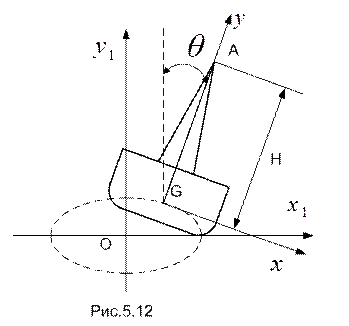
РЕШЕНИЕ. Примем за полюс центр тяжести судна – точку G. В момент времени 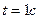координаты полюса и угол крена равны:

;

.

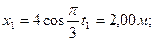
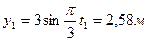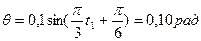Проекции скорости и ускорения полюса на оси неподвижной координатной системы при 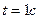имеют значения:

.

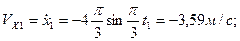
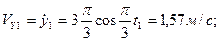
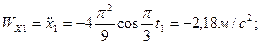
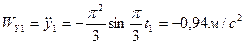Значение угловой скорости и ускорения при :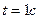

.

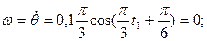
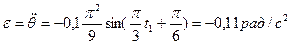Для скорости точки А можно записать .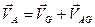

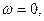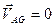Поскольку в рассматриваемый момент то и .

Для ускорения точки А справедливо равенство .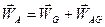

На рис.5.13 показаны найденные выше составляющие ускорения полюса 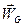, а так же вращательная составляющая ускорения :

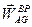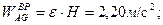( так как ).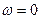

Из рисунка следует:

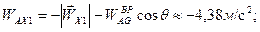
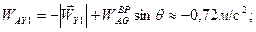
Отсюда получаем

.

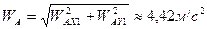Date: 2015-09-03; view: 507; Нарушение авторских прав