Расчет глобальных и локальных кинематических характеристик в случае движения мгновенной оси по конической поверхности

Существует широкий круг задач, в которых положение мгновенной оси достаточно очевидно для любого момента времени. В качестве примеров рассмотрим изображенные на рис.4.1.б,в конус и гироскоп. Так для конуса, катящегося без проскальзывания по горизонтальной поверхности, мгновенная ось вращения в любой момент времени совпадает с линией соприкосновения конуса и поверхности. Совокупность этих линий образует плоскость, которая есть частный случай конической поверхности с телесным углом при вершине в 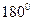. Очевидно, что при равномерном качении конуса годограф конца вектора угловой скорости вычерчивает окружность, а при ускоренном – спираль на конической поверхности.

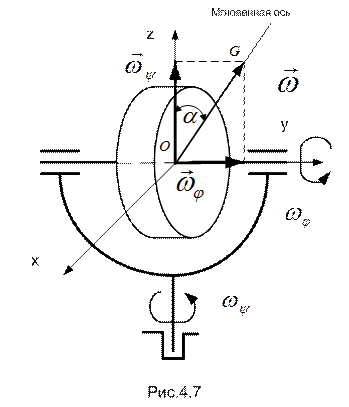
Для гироскопа с двумя степенями свободы (см. рис.4.7) при его равномерном вращении вокруг собственной и вертикальной

осей () угол между вектором мгновенной оси вращения и вертикалью в процессе движения не изменяется, т.е. положения вектора образуют коническую поверхность с углом при вершине . При этом годограф точки G – конца вектора угловой скорости, представляет собой окружность, расположенную в горизонтальной плоскости.

Сопоставив формулы для вычисления скорости точки 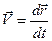и углового ускорения 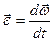можно заметить одинаковость их структуры, и, как следствие, сделать вывод о возможности аналогичного получения результатов. Так, если вектор 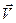совпадает с касательной к траектории движения точки (годограф вектора ), то и направление вектора 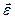должно совпадать с направлением касательной к годографу вектора 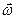. При известном движении мгновенной оси может быть определена скорость движения точки G конца вектора 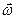, а так же равное ей угловое ускорение сферического движения, т.е. .

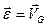Заметим, что вектор 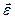приложен в неподвижной точке О, а 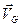- в точке G.

Приведенный подход существенно упрощает расчет углового ускорения для довольно широкого круга задач практики, рассматривающих, по своей сути, качение без проскальзывания одной конической поверхности по другой, неподвижной.

ПРИМЕР 4.3. Коническое зубчатое колесо радиуса 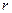катится по неподвижному зубчатому колесу радиуса 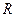; угол между осями колес составляет 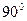(см. рис.4.8). Время одного оборота относительно вертикальной оси постоянно и равно Т. Найти угловую скорость 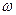и угловое ускорение 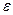колеса, а так же скорость 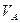и ускорение 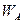его верхней точки А.

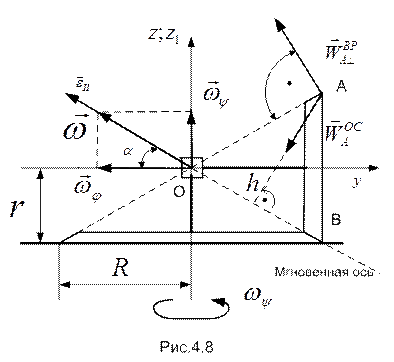
РЕШЕНИЕ. Угловая скорость прецессии колеса 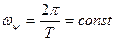. Угол нутации постоянен и равен 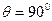, т.е. 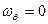. В этом случае . Построив соответствующий параллелограмм угловых скоростей (сторона 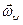известна, линия вектора совпадает с осью подвижного колеса, линия мгновенной оси проходит через две неподвижные точки – точку О и точку В контакта с неподвижным колесом), получим:

, .

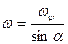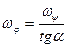При движении колеса вектор мгновенной угловой скорости поворачивается вокруг вертикальной оси, образуя коническую поверхность с углом при вершине (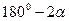); поскольку 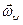и направления векторов 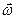и в подвижной системе осей не изменяются, не изменяется и модуль вектора 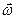. В этом случае ; .

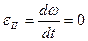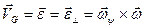Вектор углового ускорения приложен в точке О и направлен на нас перпендикулярно плоскости рисунка. Модуль углового ускорения равен

.

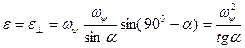Опустив из точки А на мгновенную ось перпендикуляр, найдем кратчайшее расстояние от точки до линии вектора 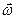как

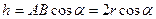. Тогда вектор скорости точки А будет направлен перпендикулярно плоскости рисунка в противоположную от нас сторону, а его модуль будет равен

.

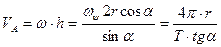Осестремаительная составляющая ускорения точки А направлена от точки к мгновенной оси (см. рисунок), а ее модуль равен

.

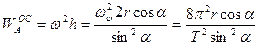Вращательная составляющая ускорения, равная

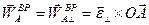, расположена в плоскости рисунка и составляет угол 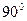c 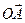(см. рисунок). Ее модуль равен

.

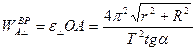Обе компоненты ускорения лежат в плоскости рисунка и составляют между собой угол (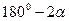). Тогда

.

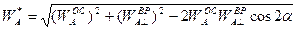Рассмотрим теперь более общий случай, когда вращение конического колеса вокруг вертикальной оси ускоренное (в этом случае полагаются известными величины угловой скорости 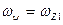и углового ускорения 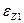вращательного движения вокруг вертикальной оси).

Если в рамках предыдущих исходных данных параллелограмм угловых скоростей равномерно вращался вокруг вертикальной оси без изменения размеров своих сторон, то в рассматриваемом случае, во-первых, вращение будет ускоренным, и, во-вторых, стороны будут возрастать, сохраняя при этом выведенные ранее соотношения. Так же остаются справедливыми формулы для расчета 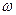, , 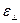, 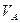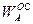и .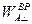

Продифференцировав формулу для расчета угловой скорости, получим:

.

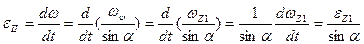Тогда вектор

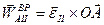перпендикулярен плоскости рисунка и направлен в противоположную от нас сторону, а его модуль .

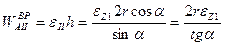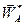Полное ускорение точки А будет результатом сложения двух ортогональных векторов и 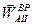, т.е.

.

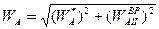Date: 2015-09-03; view: 372; Нарушение авторских прав