Основные соотношения между локальными и глобальными кинематическими характеристиками

Как и в параграфе 3.2 связь между скоростью точки М тела и угловой скоростью 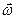(рис.4.4) имеет вид

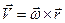(4.5)

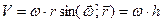
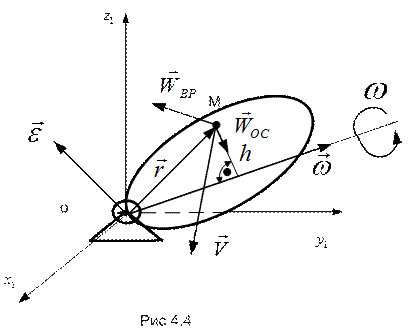
Ускорение получают путем дифференцирования (4.5) по времени:

. (4.6)

Как и в параграфе 3.2, составляющие ускорения 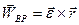и 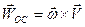называются, соответственно, вращательной и осестремительной. Однако если при вращении вокруг неподвижной оси вращательная составляющая ускорения оказывалась одновременно касательной составляющей, а осестремительная – нормальной, то при сферическом движении этого совпадения, вообще говоря, нет.

ПРИМЕР 4.2. Судно совершает бортовую качку 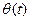, вращаясь вокруг практически неподвижной продольной оси судна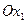

(см. рис.4.5). В диаметральной плоскости судна вокруг оси 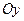вращается равномерно с угловой скоростью 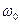диск гироскопического успокоителя качки. Известен радиус диска 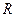и мгновенные значения угловой скорости 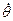и углового ускорения .

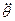Определить скорость и ускорение точки А диска.

РЕШЕНИЕ. Неподвижная система осей 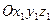и система осей 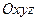, связанная с гироскопом, показаны на рис.4.5. Гироскоп участвует в двух вращениях: относительно неподвижной оси 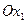и относительно поворачивающейся оси 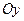с угловыми скоростям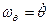и и 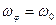соответственно (см. рис.4.6).

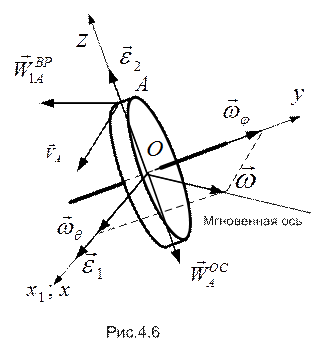
Таким образом, гироскоп совершает сферическое движение с мгновенной угловой скоростью 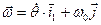, модуль которой . Мгновенная ось вращения проходит через неподвижную точку О и лежит в плоскости .

Угловое ускорение состоит из двух составляющих:

.

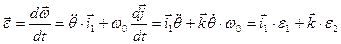(при дифференцировании подвижного орта использована формула (1.12)).

Запишем формулу для вычисления скорости точки А обода гироскопа: .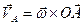

Тогда ее модуль равен .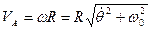

Ускорение точки А состоит из трех составляющих:

;

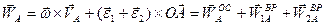где .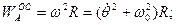

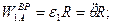
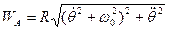В формуле учтено, что 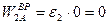, так как точка А лежит на линии вектора 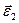. Векторы скорости и составляющих ускорения нанесены на рис.4.6.

Заметим, что в общем случае составляющие ускорения точки тела, совершающего сферическое движение, могут быть не ортогональными.

4.4.Матрица ориентации, связь глобальных кинематических характеристик с элементами матрицы вращения и углами Эйлера *

Взаимную ориентацию ортов подвижной 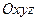и неподвижной 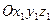систем осей можно задать таблицей направляющих косинусов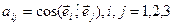

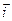
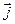
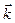
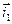
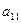
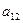
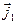
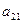
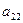
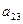
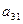
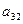
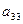
Составленную из направляющих косинусов 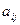матрицу А называют матрицей ориентации (или матрицей вращения). Например, если ос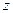и и 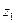тождественно совпадают (см. в параграфе 3.2 поворот вокруг неподвижной оси 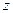), эта матрица 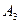имеет вид

.

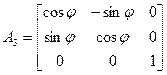Из курса высшей алгебры известно, что все матрицы вращения обладают двумя полезными свойствами:

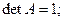
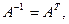
где 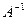- матрица, обратная 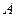, 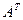- транспонированная матрица .

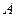Матрицы вращения позволяют получить удобный вид записи связей между столбцами ортов неподвижной и подвижной систем осей (или столбцами соответствующих координат):

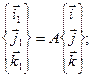
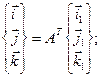
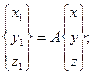
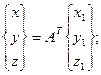(4.7)

Для того, чтобы определить зависимость элементов 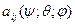от эйлеровых углов, вновь обратимся к рис.4.3, где показаны начальные положения осей (нижние индексы - единица), промежуточные (верхние индексы - два штриха либо один), а так же окончательные положения (индексы отсутствуют). Там же приводятся соответствующие матрицы ориентации для каждого из поворотов. Следуя выражениям (4.7), для промежуточных ортов получим:

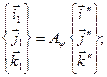
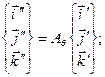
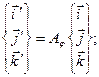
Последовательно исключая промежуточные орты, находим

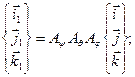так что 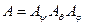. (4.8)

Применяя корабельные углы, получают матрицу

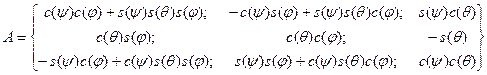Здесь для краткост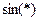и и 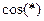обозначены символам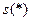и и .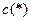

При малых наклонениях корабля 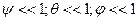можно принять, что синусы малых углов равны самим углам, а косинусы этих углов равны единице. В этом случае элементы матрицы ориентации линейно зависят от углов :

.

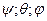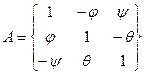В предыдущих параграфах малое перемещение тела с одной неподвижной точкой представлено в виде трех последовательных малых поворотов 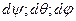. Каждый поворот характеризует свой вектор угловой скорости 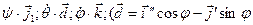- единичный вектор линии узлов ОК, показанный на рис.4.2.б и 4.3.г). Сложим векторы угловых скоростей и получим проходящий через неподвижную точку О тела вектор суммарной угловой скорости :

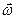(4.9)

а значит, и положение мгновенной оси (рис.4.4).

Используя первую из формул преобразования (4.7)

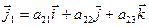и выписанное выше выражение орта 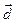, находят компоненты вектора 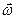в подвижном базисе:

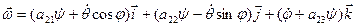. (4.10)

Отсюда можно записать кинематические уравнения А.Н.Крылова в подвижном базисе:

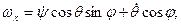
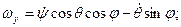(4.11)

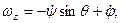
Используя матрицу вращения, получим проекции вектора угловой скорости на неподвижные оси:

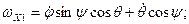
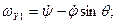(4.12)

.

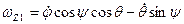Формулы для вычисления компонент вектора углового ускорения в неподвижном базисе могут быть получены путем дифференцирования по времени выражений (4.12):

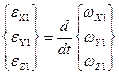. (4.13)

Отметим, что соотношение

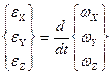
Написанное по аналогии с (4.13) для подвижного базиса было бы неверным, так как не учитывает переменности ортов вследствии вращения вокруг мгновенной оси. Поэтому компоненты вектора углового ускорения в подвижном базисе определяются с помощью матрицы вращения по правилу

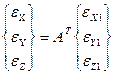. (4.14)

Date: 2015-09-03; view: 516; Нарушение авторских прав