Умови завдання

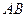Варіанти 00 - 09. Тіло рухається з точки (рис.Д1.0) по ділянці (довжиною 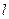) похилої площини, що становить кут з горизонтом, протягом 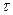сек. Його початкова швидкість . Коефіцієнт тертя ковзання тіла по площині дорівнює .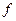

В точці 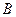тіло із швидкістю 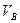залишає площину і попадає зі швидкістю в точку площини 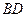, нахиленої під кутом 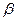до горизонту, знаходячись у повітрі 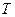сек.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.0.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.0.

При розв’язанні задачі тіло вважати матеріальною точкою. Опір повітря не враховувати.

Табл.Д1.0.

№ вар.	Дано	Визначити
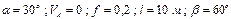
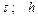
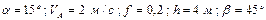
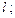		рівняння траекторії на ділянці

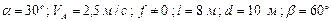
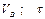
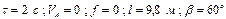
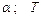
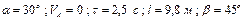
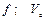
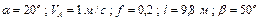
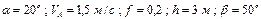
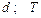
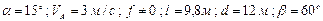
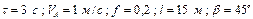
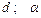
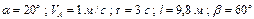
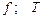
Варіанти 10 - 19. Лижник підходить до точки (рис.Д1.1) ділянки трампліна 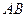, що нахилена під кутом до горизонту і має довжину 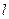, зі швидкістю . Коефіцієнт тертя ковзання лиж на ділянці 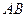дорівнює 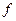. Лижник від до 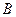рухається 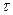сек. В точці 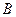зі швидкістю 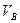він залишає трамплін і через 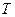сек приземляється зі швидкістю в точці гори, що становить кут 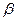з горизонтом.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.1.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.1.

При розв’язанні задачі прийняти лижника за матеріальну точку. Опір повітря не враховувати.

Табл.Д1.1.

№ вар.	Дано	Визначити
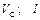
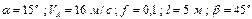
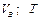
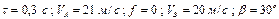
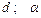
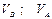
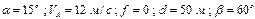
		рівняння траекторії на ділянці

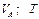
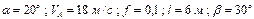
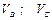
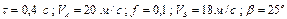
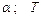
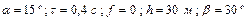
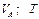
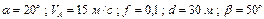
Варіанти 20 - 29. Маючи в точці (рис.Д1.2) швидкість , мотоцикл піднімається 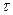сек по ділянці 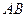довжиною 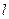, що становить з горизонтом кут . При постійній на всій ділянці 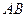рушійній силі 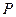мотоцикл в точці 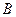набуває швидкості 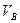і перелітає через рів шириною 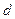, знаходячись у повітрі 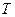сек і приземляючись в точці зі швидкістю . Маса мотоцикла з мотоциклістом дорівнює .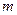

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.2.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.2.

При розв’язанні задачі прийняти мотоцикл з мотоциклістом за матеріальну точку. Сили опору руху не враховувати.

Табл.Д1.2.

№ вар.	Дано	Визначити

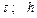
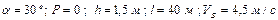
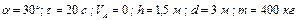
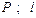
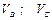
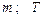
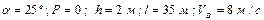
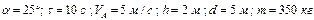
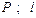
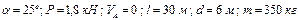
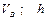
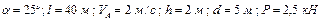
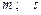
Варіанти 30 - 39. Камінь (рис.Д1.3) сковзає протягом 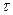сек по ділянці 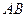похилої площини, що складає кут з горизонтом і має довжину 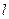. Його початкова швидкість . Коефіцієнт тертя ковзання каменю по площині дорівнює 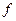. Маючи в точці 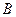швидкість 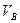, камінь через 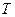сек вдаряється в точці об вертикальну стіну.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.3.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.3.

При розв’язанні задачі прийняти камінь за матеріальну точку. Опір повітря не враховувати.

Табл.Д1.3.

№ вар.	Дано	Визначити

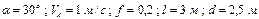
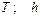
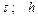
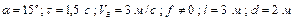
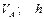
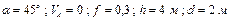
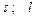
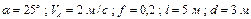
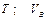
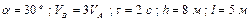
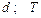
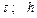
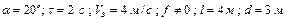
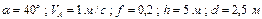
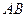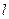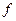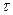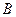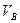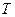Варіанти 40 - 49. Тіло (рис.Д1.4) рухається з точки по ділянці (довжиною ) похилої площини, що складає кут з горизонтом. Його початкова швидкість . Коефіцієнт тертя ковзання дорівнює . Через сек тіло в точці зі швидкістю залишає похилу площину і падає на горизонтальну площину в точку зі швидкістю . При цьому тіло перебуває в повітрі сек.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.4.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.4.

При розв’язанні задачі прийняти тіло за матеріальну точку. Опір повітря не враховувати.

Табл.Д1.4.

№ вар.	Дано	Визначити
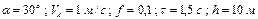
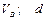
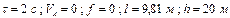
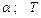
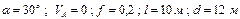
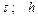
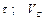
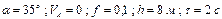
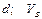
		рівняння траекторії на ділянці
		рівняння траекторії на ділянці

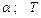
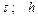
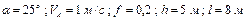
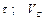
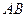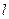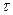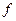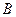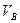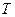Варіанти 50 - 59. Маючи в точці (рис.Д1.5) швидкість , тіло рухається по горизонтальній ділянці довжиною протягом сек. Коефіцієнт тертя ковзання тіла по площині дорівнює . В точці зі швидкістю тіло залишає площину і попадає в точку зі швидкістю , знаходячись у повітрі сек.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.5.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.5.

При розв’язанні задачі прийняти тіло за матеріальну точку. Опір повітря не враховувати.

Табл.Д1.5.

№ вар.	Дано	Визначити
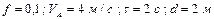
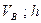
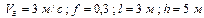
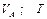
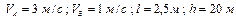
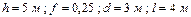
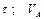
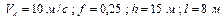
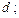		рівняння траекторії на ділянці

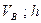
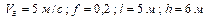
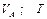
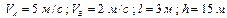
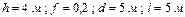
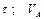
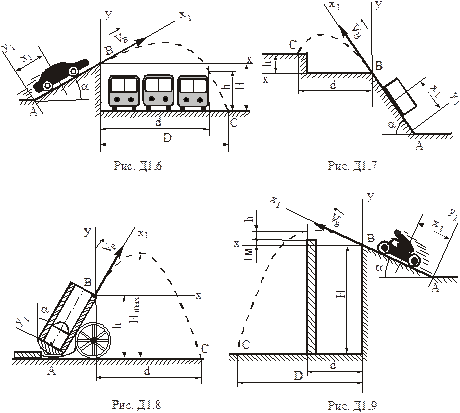
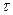Варіанти 60 - 69. Маючи в точці (рис.Д1.6) швидкість , автомобіль з каскадером піднімаються сек по ділянці 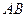трампліна довжиною 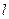, що становить з горизонтом кут . При постійній на всій ділянці 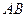рушійній силі 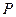автомобіль в точці 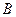набуває швидкості 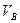, покидає трамплін і перелітає через перешкоду, приземляючись в точці на відстані 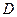від трампліна. В момент подолання перешкоди (на відстані 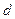від трампліна) автомобіль знаходиться на висоті 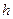від поверхні землі і перебуває в повітрі 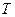сек. Висота трампліна 4 м. Маса автомобіля з каскадером дорівнює .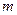

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.6.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.6.

При розв’язанні задачі прийняти автомобіль з каскадером за матеріальну точку. Сили опору руху не враховувати.

Табл.Д1.6.

№ вар.	Дано	Визначити
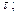		рівняння траекторії на ділянці
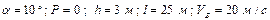
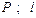
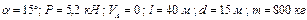
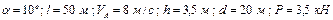
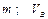
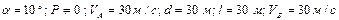
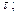		рівняння траекторії на ділянці
		рівняння траекторії на ділянці

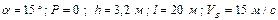
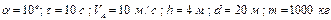
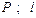
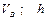
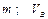
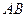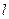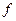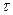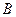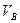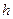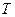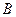Варіанти 70 - 79. Тіло (рис.Д1.7) рухається з точки по ділянці (довжиною ) похилої площини, що складає кут з горизонтом. Його початкова швидкість . Коефіцієнт тертя ковзання дорівнює . Через сек тіло в точці зі швидкістю залишає похилу площину і падає на горизонтальну площину на висоті в точку зі швидкістю . При цьому тіло знаходиться в повітрі сек, а точка віддалена від точки на відстані .

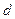Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.7.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.7.

При розв’язанні задачі прийняти тіло за матеріальну точку. Опір повітря не враховувати.

Табл.Д1.7.

№ вар.	Дано	Визначити

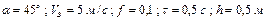
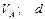
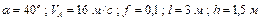
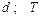
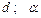
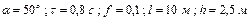
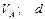
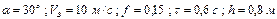
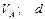
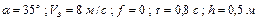
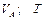
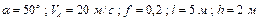
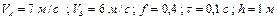
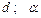
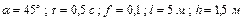
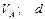
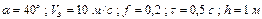
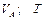
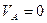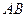Варіанти 80 - 89. Артилерійський снаряд стартує () із точки (рис.Д1.8) ствола гармати. Ствол нахилений під кутом до вертикалі і має довжину 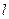. Від до 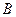снаряд рухається 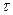сек під дією постійної сили 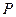тиску порохових газів. В точці 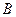зі швидкістю 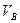він залишає ствол і через 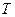сек польоту попадає зі швидкістю в точку , що знаходиться на відстані 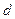від гармати. Точка 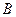гармати знаходиться на висоті 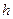від поверхні Землі. При русі по траєкторії снаряд досягає максимальної висоти 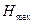за час 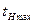від моменту вильоту з гармати.

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.8.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.8.

При розв’язанні задачі прийняти снаряд за матеріальну точку. Опір повітря не враховувати. Поверхню Землі вважати плоскою.

Табл.Д1.8.

№ вар.	Дано	Визначити
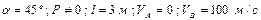
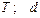
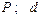
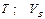
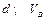
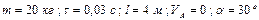
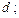		рівняння траекторії на ділянці

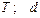
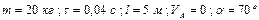
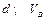
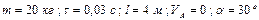
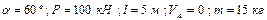
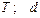
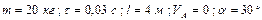
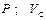
Варіанти 90 - 99. Маючи в точці (рис.Д1.9) швидкість , мотоцикл з мотоциклістом піднімаються 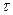сек по ділянці 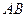трампліна довжиною 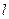, що складає з горизонтом кут . При постійній на всій ділянці 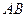рушійній силі 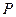мотоцикл в точці 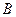набуває швидкості 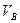, залишає трамплін і перелітає через перешкоду, приземляючись в точці на відстані 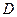від трампліна. В момент подолання перешкоди (на відстані 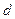від трампліна) мотоцикл знаходиться вище перешкоди на 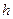(м), а час польоту в цю мить складає 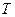сек. Висота трампліна 3 м. Висота перешкоди 4 м. Маса автомобіля з каскадером дорівнює .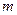

Числові параметри, що задаються, приведені в стовпці «Дано» табл.Д1.9.

Визначити: параметри, зазначені в стовпці «Визначити» табл.Д1.9.

При розв’язанні задачі прийняти мотоцикл з мотоциклістом за матеріальну точку. Сили опору руху не враховувати.

Табл.Д1.9.

№ вар.	Дано	Визначити

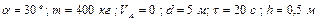
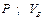
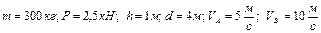
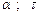
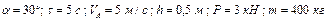
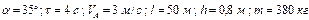
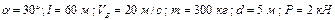
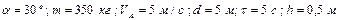
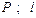
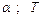
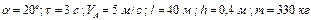
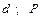
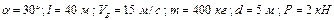
Теоретичне обґрунтування: [5] § 79, 80, 82; [6] Розд.III. Гл.1. § 4 -7; [7] § 5 -7; [8]; [9].

Методичні вказівки. Завдання Д-1 на тему “Динаміка матеріальної точки” і полягає у визначенні закону руху точки шляхом інтегрування диференціальних рівнянь руху.

У загальному випадку рух точки під дією однієї або кількох сил може бути визначений за допомогою основного закону динаміки, який пов’язує діючі на точку сили, масу точки та її прискорення. У векторній формі цей зв’язок має вигляд:

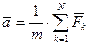(Д1.1)

де 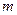- маса точки;

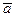- прискорення точки;

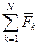- векторна сума сил, що діють на точку.

Якщо спроектувати (Д1.1) на осі 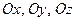прямокутної системи координат будемо мати:

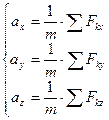(Д1.2)

Ураховуючи, що 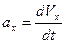, , 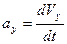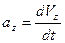отримаємо проекції швидкості точки у будь-який момент часу:

, (Д1.3)

де 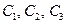- константи інтегрування, які визначаються з початкових умов.

Повний вектор швидкості є геометричною сумою його проекцій, а величина може бути визначена за формулою:

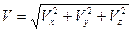
Якщо треба отримати координати 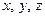точки як функції часу, слід зробити заміну 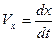, , 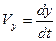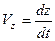. Тоді маємо наступне:

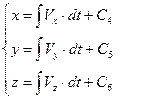, (Д1.4)

де 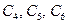- константи інтегрування, які визначаються з початкових умов.

Таким чином, при відомих силах, що діють на точку, і її масі, рух точки і її положення в кожну мить можуть бути визначеними за формулами (Д1.2) - (Д1.4).

Якщо рух точки відбувається в площині, достатньо користуватися двома координатними осями. Якщо рух точки є прямолінійним – обмежуються однією чи двома осями.

В запропонованому завданні рух точки спостерігається в площині на двох ділянках – прямолінійній і криволінійній. Для складання диференціальних рівнянь руху точки на кожній з ділянок необхідно враховувати напрямок осей координат (задані на рисунку) і сили, що діють на точку в довільний момент часу. Треба також врахувати, що точка 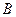є спільною для двох ділянок, тобто швидкість 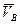є кінцевою для першої ділянки і початковою для другої. Константи інтегрування знаходять з початкових умов для кожної з ділянок. Отримані розв’язки диференціальних рівнянь дозволяють знайти шукані величини.

Якщо при розв’язанні задачі виникає проблема недостачі вихідних даних, то необхідно отримати в загальному вигляді швидкості і координати точки на обох ділянках, а потім розв’язати систему алгебраїчних рівнянь відносно усіх невідомих, що входять в ці рівняння.

Date: 2015-09-03; view: 446; Нарушение авторских прав