К каноническому виду

Квадратичной формой переменных 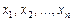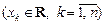называется однородный многочлен второй степени относительно этих переменных:

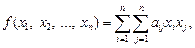(23.20)

где 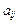– числовые коэффициенты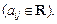

Квадратичная форма (23.20) не содержит свободного члена и одночленов 1-й степени.

Квадратичную форму можно записать так, что коэффициенты пр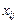и и 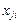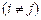будут равны, поэтому будем считать, что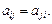

Матрица

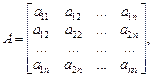(23.21)

составленная из коэффициентов квадратичной формы, называется матрицей квадратичной формы.

Квадратичная форма (23.20) может быть записана в виде

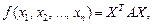(23.22)

где А – матрица (23.21),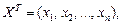

X – матрица-столбец переменных.

Если 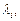– собственные числа матрицы (23.21), то квадратичная форма имеет канонический вид:

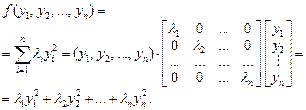(23.23)

Если 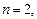то квадратичная форма (23.20) имеет вид:

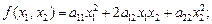(23.24)

если 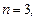то –

(23.25)

Понятие «квадратичная форма с двумя переменными» используют для приведения уравнения линии второго порядка к каноническому виду, а c тремя переменными – для приведения уравнения поверхности второго порядка к каноническому виду.

Как известно, множество точек плоскости, координаты которых удовлетворяют уравнению:

(23.26)

в декартовой системе координат 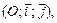называется линией второго порядка.

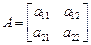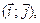
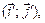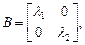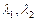Пусть дано уравнение (23.26). Рассмотрим квадратичную форму с матрицей в базисе Существует ортонормированный базис составленный из собственных векторов матрицы А, в котором матрица В квадратичной формы f имеет вид: где – собственные значения матрицы A. Сделав замену координат, приводим уравнение (23.26) к виду:

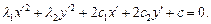(23.27)

Далее выделяем полные квадраты и приводим уравнение к каноническому уравнению кривой 2-го порядка.

Множество точек 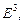координаты которых удовлетворяют уравнению:

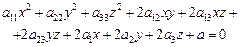(23.28)

в декартовой системе координат 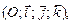называется поверхностью второго порядка в

Старшие члены уравнения (23.28) образуют квадратичную форму f с матрицей A в указанном базис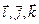е где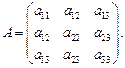

Существует ортонормированный базис 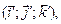составленный из собственных векторов матрицы A, в которых квадратичная форма f имеет канонический вид. Сделав замену координат, приводим уравнение (23.28) к виду:

(23.29)

где 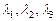– собственные значения матрицы А.

Далее выделяем полные квадраты и сводим уравнение к каноническому виду.

Пример 1. В базисе 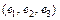задана квадратичная форма 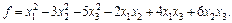Записать матрицу А формы f в этом базисе.

Решение. Учитывая, что 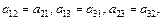записываем

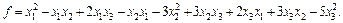
Тогда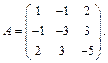

Пример 2. В базисе 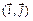пространства 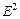задана квадратичная форма 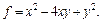Привести эту форму f к каноническому виду, выписав соответствующий базис и матрицу перехода от старого базиса к новому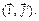

Решение. Матрица A формы f в базисе имеет следующий вид: 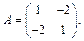Находим собственные значения и собственные векторы матрицы A:

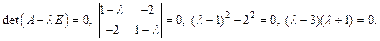
Получаем:

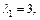
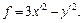
Для 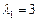имеем:

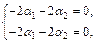откуда т. е. 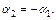Нашли собственный вектор

Для него 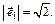Поэтому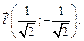

Для 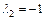имеем:

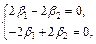откуда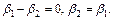

Получили собственный вектор для которого 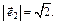Тогда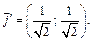

Новый базис:

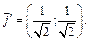
Далее:

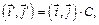где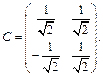

Пример 3. В базисе 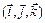пространства 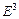задана квадратичная форма Привести эту форму f к каноническому виду, записав соответствующий базис 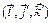и матрицу C перехода от старого базиса 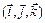к новому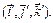

Решение. Матрица A формы f в базисе 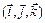имеет следующий вид: 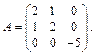Находим собственные значения и собственные векторы матрицы A:

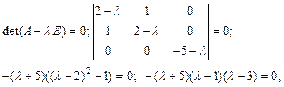
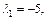
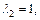
откуда Тогда

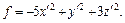
Последовательно находим:

1)

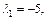
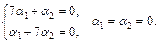
Собственный вектор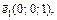

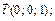
2)

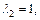
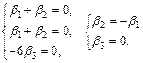
Собственный вектор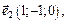

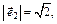
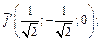
3)

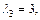
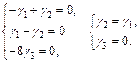
Собственный вектор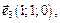

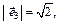
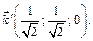
Таким образом получили новый базис: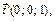

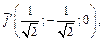
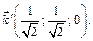
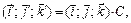
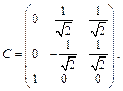
Пример 4. В некотором базисе пространства 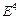задана квадратичная форма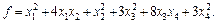

Найти канонический вид этой квадратичной формы.

Решение. Запишем матрицу формы f в этом базисе и найдем собственные значения этой матрицы A:

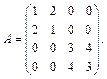
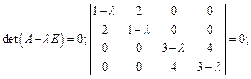
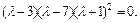
Получаем: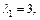

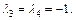
Тогда в некотором новом базисе квадратичная форма f по формуле (23.23) имеет следующий вид:

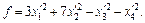
Пример 5. В системе координат xOy плоскости 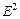задана линия второго порядка Найти каноническое уравнение этой линии в некоторой декартовой системе координат а также зависимость между координатам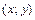и и

Решение. Рассмотрим квадратичную форму и приведем ее к каноническому виду (см. пример 2, с. 33 данного пособия):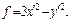

где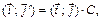

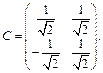
Тогда по формуле замены координат имеем:

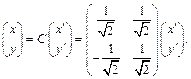Значит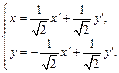

Подставляя в уравнение линии, получаем:

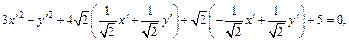
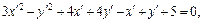
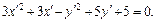
В последнем уравнении, выделив полные квадраты, получим:

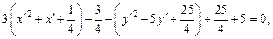
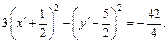
Пусть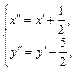

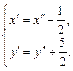
Тогда т. е. 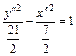– уравнение гиперболы.

Зависимость между старыми и новыми координатами задается равенствами:

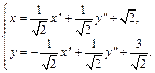
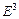Пример 6. В системе координат пространства задана поверхность второго порядка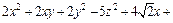 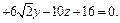Найти каноническое уравнение этой поверхности в некоторой декартовой системе координат 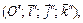а также зависимость между координатами (x; y; z) и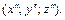

Решение. Рассмотрим квадратичную форму 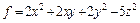и приведем ее к каноническому виду (см. пример 3, с. 34 данного пособия): 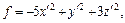где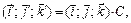

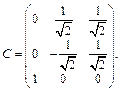
Согласно формуле замены координат имеем:

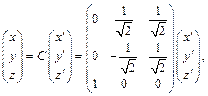
откуда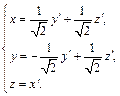

Подставляя в уравнение поверхности, получаем:

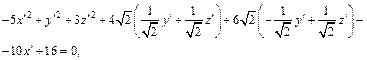
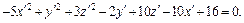
Выделяя полные квадраты, получим:

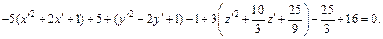
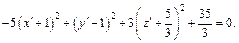
Пусть 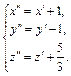Тогда получаем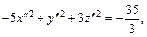

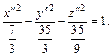
Приходим к уравнению

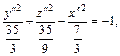
которое определяет двуполостный гиперболоид.

Переход к каноническому виду уравнения был произведен с помощью следующих преобразований координат:

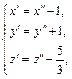т. е.

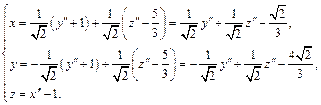
Date: 2015-09-03; view: 1302; Нарушение авторских прав