
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

И примеры
|
|
Пусть V – линейное пространство. Каждой паре векторов 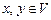 поставим в соответствие действительное число (обозначим (x, y) или
поставим в соответствие действительное число (обозначим (x, y) или  ), называемое скалярным произведением векторов x, y и удовлетворяющее следующим аксиомам:
), называемое скалярным произведением векторов x, y и удовлетворяющее следующим аксиомам:
E1) скалярное произведение векторов x, y коммутативно, т. е. 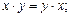
E2) скалярное произведение векторов дистрибутивно относительно сложения векторов, т. е. 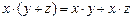 для любых
для любых 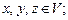
E3) числовой множитель 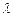 можно выносить за знак скалярного произведения, т. е.
можно выносить за знак скалярного произведения, т. е. 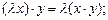
E4) скалярный квадрат 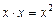 вектора
вектора  неотрицателен, т. е.
неотрицателен, т. е.  причем
причем  тогда и только тогда, когда
тогда и только тогда, когда 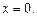
Линейное пространство V со скалярным произведением, удовлетворяющим аксиомам E1)–E4), называется евклидовым пространством и обозначается Е, n-мерное евклидово пространство обозначается 
Теорема (неравенство Коши–Буняковского). Для любых двух векторов x, y евклидова пространства E справедливо неравенство: 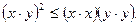
В евклидовом пространстве E для любого вектора x определяется длина (норма) этого вектора:
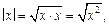
обладающая следующими свойствами:
D1) 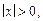 если
если 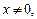 и
и 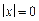 тогда и только тогда, когда
тогда и только тогда, когда 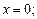
D2) 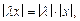
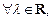
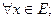
D3) 
 (неравенство треугольника).
(неравенство треугольника).
В евклидовом пространстве E для любых векторов x, y определяется угол 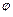
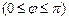 между векторамиx, y, косинус которого находится по формуле:
между векторамиx, y, косинус которого находится по формуле:
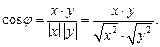
Два вектора евклидова пространства E называются ортогональными, если их скалярное произведение равно нулю.
Система векторов называется ортогональной, если каждая пара векторов этой системы ортогональна.
Вектор, длина которого равна единице, назывется нормированным. Для любого вектора 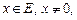 нормированный вектор
нормированный вектор  находится по формуле:
находится по формуле: 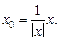
Базис 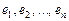 евклидова пространства
евклидова пространства 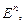 который удовлетворяет условиям
который удовлетворяет условиям  (
(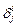 – символ Кронекера), называется ортонормированным базисом.
– символ Кронекера), называется ортонормированным базисом.
Базис 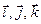 трехмерного пространства геометрических векторов является ортонормированным.
трехмерного пространства геометрических векторов является ортонормированным.
Пусть 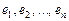 – ортонормированный базис пространства
– ортонормированный базис пространства 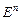 и векторы
и векторы 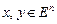 разлагаются по векторам этого базиса:
разлагаются по векторам этого базиса:
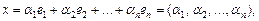
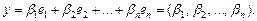
Тогда имеем:
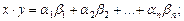 (23.3)
(23.3)
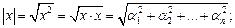 (23.4)
(23.4)
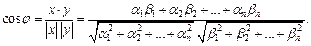 (23.5)
(23.5)
Пример 1. Доказать, что евклидовым пространством является:
1) множество всех геометрических векторов 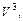 если скалярное произведение векторов
если скалярное произведение векторов 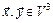 задать по формуле
задать по формуле 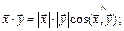
2) множество 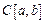 всех действительных функций, определенных и непрерывных на отрезке
всех действительных функций, определенных и непрерывных на отрезке 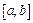 со скалярным произведением
со скалярным произведением 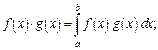
3) арифметическое линейное пространство 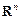 относительно скалярного произведения, определяемого по формуле
относительно скалярного произведения, определяемого по формуле 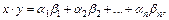 где
где 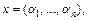
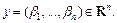
Решение. Проверка аксиом Е1)–Е4) осуществляется в любом курсе аналитической геометрии.
Выполнение аксиом E1)–E4) следует из свойств определенного интеграла.
Непосредственно проверяется справедливость аксиом E1)–E4).
Пример 2. Доказать, что ортогональная система векторов 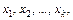 не содержащая нулевых векторов, состоит из линейно-независимых векторов.
не содержащая нулевых векторов, состоит из линейно-независимых векторов.
Решение. Пусть 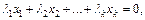 тогда
тогда
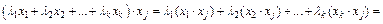
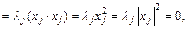
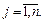 Если
Если 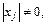
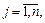 то
то  Следовательно, векторы
Следовательно, векторы  – линейно-независимые.
– линейно-независимые.
Пример 3. Найти угол между векторами 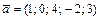 и
и 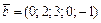 в
в 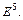
Решение. Используя формулы (23.3)–(23.5), находим:
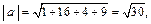
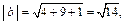
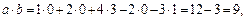
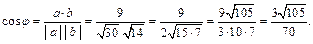
Получаем 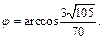
Date: 2015-09-03; view: 409; Нарушение авторских прав