Линейного оператора. Число называется собственным значением оператора A, если существует ненулевой вектор такой, что

Число 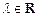называется собственным значением оператора A, если существует ненулевой вектор такой, что

(23.15)

Вектор x, удовлетворяющий условию (23.15), называется собственным вектором оператора A, соответствующим собственному значению l. Множество всех собственных значений оператора A называется его спектром.

Пусть 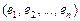– базис линейного пространства 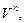A – матрица оператора A в этом базисе, 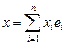– собственный вектор оператора A, X – столбец координат вектора x. Тогда условие (23.15) в матричной форме принимает вид или 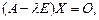где E – единичная матрица, O – нулевая матрица. Матричное уравнение 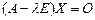представляет собой однородную систему уравнений:

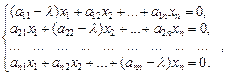(23.16)

Система уравнений (23.16) имеет отличное от нуля решение тогда и только тогда, когда:

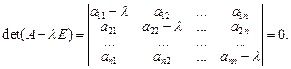(23.17)

Уравнение n -й степени (23.17) относительно переменной l называется характеристическим уравнением линейного оператора А (матрицы А). Корни этого уравнения и являются собственными значениями оператора А.

Пусть из уравнения (23.17) найден корень 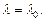Чтобы найти собственные векторы оператора А, соответствующие этому собственному значению, нужно подставить 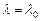в (23.16) и, решив полученную однородную систему линейных уравнений, найти координаты искомых собственных векторов.

Пример 1. Найти собственные значения и собственные векторы оператора А, заданного в некотором базисе 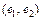пространства 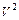матрицей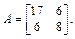

Решение. Составляем характеристическое уравнение (23.17) для заданной матрицы

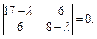
Вычисляя определитель, имеем уравнение:

т. е.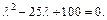

Находим 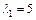и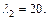

Получили собственные значения: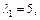

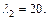
Найдем собственные векторы, соответствующие этим собственным значениям. Запишем систему уранений (23.16) для данного случая:

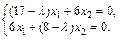(23.18)

Подставив 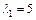в (23.18), получим систему:

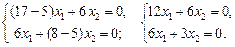
Решение системы: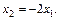

Получили множество собственных векторов, соответствующих собственному значению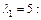

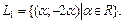
Подставив 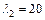в (23.18), получим однородную систему уравнений:

решив которую, имеем 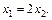Тогда множество собственных векторов, соответствующих собственному значению 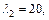будет

Пример 2. Найти собственные значения и собственные векторы оператора А, заданного в некотором базисе пространства 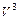матрицей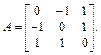

Решение. Составляем характеристическое уравнение (23.17) для заданной матрицы:

Получаем собственные значения: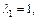

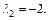
Найдем собственные векторы, соответствующие этим собственным значениям. Запишем соответствующую систему уравнений

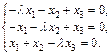(23.19)

Подставляя 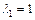в систему уравнений (23.19), получим однородную систему линейных уравнений:

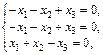
решение которой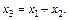

Получаем множество собственных векторов, соответствующих собственному значению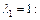

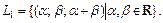
Подставляя 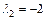в систему уравнений (23.19), получаем однородную систему линейных уравнений:

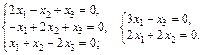
Ее решением будет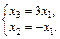

Получили множество собственных векторов, соответствующих собственному значению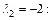

Date: 2015-09-03; view: 473; Нарушение авторских прав