
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейное пространство, определение и примеры
|
|
Пусть F – множество всех действительных чисел R или множество всех комплексных чисел C.
Множество V элементов x, y, z, … называется линейным (векторным) пространством над числовым множеством F, если для каждых двух элементов x и y из V определена их сумма  для каждого
для каждого  и каждого числа
и каждого числа 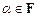 определено их произведение
определено их произведение 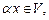 причем выполняются следующие аксиомы:
причем выполняются следующие аксиомы:
А1) 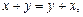
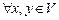 – коммутативность сложения;
– коммутативность сложения;
А2) 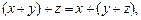
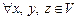 – ассоциативность сложения;
– ассоциативность сложения;
А3) существует такой элемент  называемый нулевым, что х + 0 = х,
называемый нулевым, что х + 0 = х, 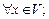
А4) для каждого элемента  существует такой элемент
существует такой элемент 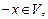 называемый противоположным к x, что
называемый противоположным к x, что 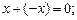
А5) 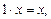
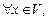
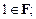
А6) 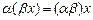 для всех
для всех  и
и 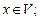
А7) 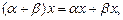
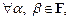
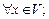
А8) 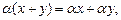
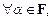

Элементы линейного (векторного) пространства называются векторами. Если F – множество действительных чисел R или множество комплексных чисел C, то векторное пространство V над множеством F называется соответственно действительным или комплексным линейным пространством. Далее, в основном, будут рассматриваться действительные линейные пространства.
Векторы 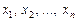 линейного пространства V называются линейно-зависимыми, если существуют числа
линейного пространства V называются линейно-зависимыми, если существуют числа 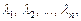 не все равные нулю, такие, что
не все равные нулю, такие, что
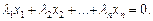 (23.1)
(23.1)
Векторы  называются линейно-независимыми, если равенство (23.1) выполняется только при условии
называются линейно-независимыми, если равенство (23.1) выполняется только при условии 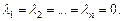
Вектор x разлагается по векторам (линейно выражается) через векторы  если
если 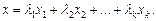 Если векторы
Если векторы  линейно-зависимы, то хотя бы один из них линейно выражается через остальные.
линейно-зависимы, то хотя бы один из них линейно выражается через остальные.
Линейно-независимая система векторов  называется базисом пространства, если любой вектор этого пространства разлагается по векторам
называется базисом пространства, если любой вектор этого пространства разлагается по векторам 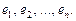 Линейное пространство называется конечномерным, если его базис состоит из конечного количества векторов, и бесконечномерным – в противном случае.
Линейное пространство называется конечномерным, если его базис состоит из конечного количества векторов, и бесконечномерным – в противном случае.
Количество n векторов базиса конечномерного пространства V называется размерностью пространства V, что записывают 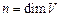 или
или 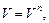 где
где 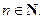
Каждую линейно-независимую систему векторов 
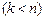 конечномерного пространства
конечномерного пространства 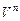 можно дополнить до базиса
можно дополнить до базиса 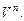
Если 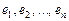 – базис пространства
– базис пространства 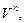 то любой вектор x из
то любой вектор x из 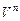 имеет единственное разложение
имеет единственное разложение
 (23.2)
(23.2)
Числа  называются координатами вектора x в базисе
называются координатами вектора x в базисе 
 при этом записывают
при этом записывают 
Если некоторое подмножество 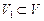 само образует линейное пространство относительно введенных в V операций сложения и умножения на число, то
само образует линейное пространство относительно введенных в V операций сложения и умножения на число, то 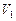 называется подпространством линейного пространства V.
называется подпространством линейного пространства V.
Пусть 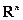 – множество всех матриц-строк, имеющих n элементов, с обычными операциями сложения матриц и умножения матрицы на число:
– множество всех матриц-строк, имеющих n элементов, с обычными операциями сложения матриц и умножения матрицы на число:
а) 
б) 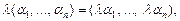
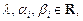
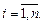
Для этого множества выполняются аксиомы А1)–А8). Следовательно, это множество является линейным пространством. Строки 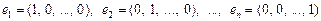 образуют базис этого пространства, поэтому оно n- мерно. Построенное пространство называется арифметическим или координатным линейным пространством и обозначается
образуют базис этого пространства, поэтому оно n- мерно. Построенное пространство называется арифметическим или координатным линейным пространством и обозначается 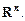
Теорема. Пусть 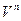 – линейное пространство размерности n. Тогда существует взаимно-однозначное соответствие между
– линейное пространство размерности n. Тогда существует взаимно-однозначное соответствие между 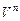 и координатным пространством
и координатным пространством 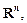
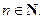
Из этой теоремы следует, что при изучении свойств пространства 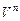 достаточно рассмотреть соответствующие свойства пространства
достаточно рассмотреть соответствующие свойства пространства 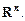
Пример 1. Показать, что множество всех многочленов 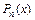 образует линейное пространство, найти базис и определить размерность пространства
образует линейное пространство, найти базис и определить размерность пространства 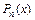 всех многочленов с коэффициентами из множества
всех многочленов с коэффициентами из множества 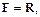 степень которых не превосходит n.
степень которых не превосходит n.
Решение. Нетрудно проверить, что множество всех таких многочленов образует линейное пространство относительно обычных операций сложения многочленов и умножения многочлена на число, т. е. выполняются аксиомы А1)–А8). Рассмотрим произвольный многочлен 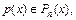 тогда
тогда 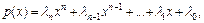
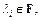
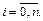 Следовательно,
Следовательно, 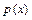 линейно выражается через многочлены
линейно выражается через многочлены 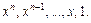 При этом
При этом 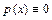 тогда и только тогда, когда
тогда и только тогда, когда 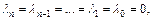 т. е.
т. е. 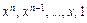 – линейно-независимые векторы, они образуют базис векторного пространства
– линейно-независимые векторы, они образуют базис векторного пространства 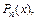 причем
причем 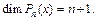
Пример 2. Определить размерность линейного пространства всех действительных функций F (R) с обычными операциями сложения функций и произведения функции на число.
Решение. Непосредственно проверяются аксиомы А1)–А8) линейного пространства, следовательно F (R) является векторным пространством. Далее, функции 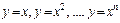 являются линейно-независимыми векторами для любого n, т. е. F (R) не имеет конечного базиса и является бесконечномерным.
являются линейно-независимыми векторами для любого n, т. е. F (R) не имеет конечного базиса и является бесконечномерным.
Пример 3. Доказать, что множество M (m, n) всех прямоугольных действительных (размера 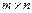 ) матриц с обычными операциями сложения матриц и умножения матрицы на число является линейным пространством. Найти его размерность.
) матриц с обычными операциями сложения матриц и умножения матрицы на число является линейным пространством. Найти его размерность.
Решение. Поскольку выполняются аксиомы А1)–А8), то M (m, n) – линейное пространство (убедитесь в этом самостоятельно).
Рассмотрим матрицу 
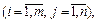 в которой элемент, стоящий в i -й строке и j -м столбце, равен 1, а все остальные элементы равны нулю. Всего таких матриц будет
в которой элемент, стоящий в i -й строке и j -м столбце, равен 1, а все остальные элементы равны нулю. Всего таких матриц будет 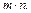 Для любой матрицы
Для любой матрицы 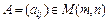 имеем:
имеем: 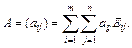 Из этого равенства следует, что любая матрица А линейно выражается через матрицы
Из этого равенства следует, что любая матрица А линейно выражается через матрицы 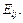 Если
Если 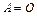 (нулевая матрица), то
(нулевая матрица), то 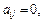
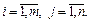 Следовательно, векторы
Следовательно, векторы 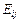 – линейно-независимы и образуют базис векторного пространства M (m, n). Таким образом, размерность этого пространства равна
– линейно-независимы и образуют базис векторного пространства M (m, n). Таким образом, размерность этого пространства равна 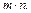 В частности, для квадратных матриц порядка n она равна
В частности, для квадратных матриц порядка n она равна 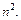
Пример 4. Доказать, что множество всех геометрических векторов в трехмерном пространстве образует трехмерное векторное пространство V.
Решение. Если рассмотреть в трехмерном пространстве декартову систему координат с соответствующими ортами 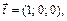
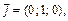
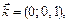 то любой вектор
то любой вектор 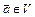 единственным образом разлагается по
единственным образом разлагается по 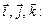
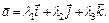
В стандартном курсе векторной алгебры показывается, что операции сложения векторов и умножения вектора на действительное число 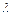 удовлетворяют аксиомам А1)–А8). Поэтому множество всех геометрических векторов V образует линейное пространство.
удовлетворяют аксиомам А1)–А8). Поэтому множество всех геометрических векторов V образует линейное пространство.
Очевидно, что в случае равенства 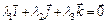 выполняется
выполняется 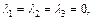 и векторы
и векторы 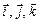 – линейно-независимы. Таким образом, пространство V имеет размерность 3 и отождествляется с
– линейно-независимы. Таким образом, пространство V имеет размерность 3 и отождествляется с 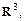 если задан базис
если задан базис 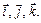
Пример 5. Описать геометрически все подпространства линейного пространства 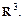
Решение. Любое векторное пространство V имеет два тривиальных подпространства V и 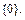 Если
Если 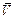 – подпространство пространства
– подпространство пространства 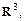 то в
то в 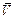 имеется максимальная система линейно-независимых векторов, предположим, что m – число векторов этой системы. Если
имеется максимальная система линейно-независимых векторов, предположим, что m – число векторов этой системы. Если  то
то 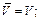 если
если 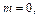 то
то 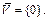 Если
Если  то
то 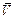 отожествляется с множеством всех векторов некоторой прямой, проходящей через начало координат. В случае
отожествляется с множеством всех векторов некоторой прямой, проходящей через начало координат. В случае 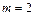 множество
множество 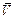 можно считать множеством всех векторов плоскости, проходящей через начало координат. Всевозможные такие прямые и плоскости геометрически и описывают все нетривиальные подпространства пространства
можно считать множеством всех векторов плоскости, проходящей через начало координат. Всевозможные такие прямые и плоскости геометрически и описывают все нетривиальные подпространства пространства 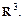
Пример 6. Доказать, что векторы 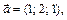
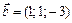 и
и 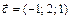 образуют базис пространства
образуют базис пространства 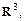 и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.
Решение. Как известно из векторной алгебры, базис в 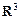 образует всякая тройка векторов, для которой смешанное произведение не равно нулю. Вычислим его для заданных векторов:
образует всякая тройка векторов, для которой смешанное произведение не равно нулю. Вычислим его для заданных векторов:
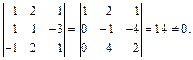
Мы убедились, что векторы 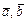 и
и 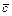 образуют базис. Чтобы определить координаты вектора
образуют базис. Чтобы определить координаты вектора 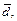 разложим его по векторам этого базиса.
разложим его по векторам этого базиса.
Предположим, что
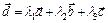
или в координатной форме
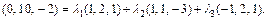
В координатной форме последнее равенство равносильно системе уравнений:
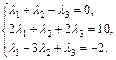
Для нахождения неизвестных коэффициентов  решим систему методом Крамера. Вычислим определитель этой системы
решим систему методом Крамера. Вычислим определитель этой системы
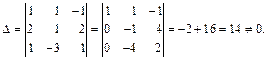
Далее находим
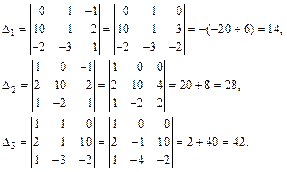
Используя формулы Крамера, находим:

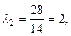
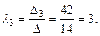
Таким образом в базисе 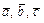 справедливо разложение
справедливо разложение 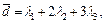 т. е.
т. е. 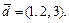
Date: 2015-09-03; view: 2081; Нарушение авторских прав