Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Без учета сопротивления
|
|
На МТ массой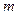 
, кроме силы тяжести 
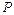и восстанавливающей силы 
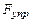, действует периодически изменяющаяся, называемая возмущающей, сила 
, где Н – ее амплитуда, р – частота, 
– начальная фаза (рис. 2.8, д). Тогда дифференциальное уравнение движения МТ
, (3.10)
или 
.
Обозначив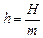 
, 
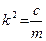(частота собственных колебаний), имеем 
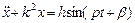. Тогда общее решение
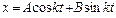
, или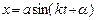 
.
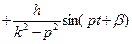Произвольные постоянные интегрирования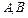 
(
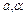) находятся с помощью начальных условий.
Амплитуда вынужденных колебаний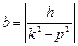 
.
Отношение амплитуды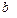 
к статической деформации 
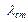называется коэффициентом динамичности: 
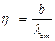. При 
> 
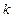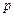вынужденные колебания и возмущающая сила находятся в одной фазе (имеют одновременно максимумы и минимумы): 
.При 
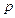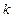> вынужденные колебания и возмущающая сила имеют противоположные фазы:
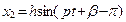. (3.19)
Вопрос 15 ЯВЛЕНИЕ РЕЗОНАНСА
Рассмотрим случай, когда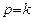 
,то естьчастота возмущающей силы совпадает с частотой собственных колебаний. Это явление называется резонансом. Дифференциальное уравнение движения
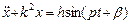. Частное решение имеет вид
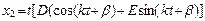. (3.21)
Приравняв коэффициенты при одноименных функциях аргумента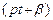 
, получим 
, 
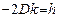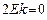, откуда 
, 
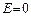.Следовательно, 
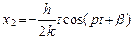, или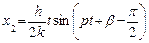 
. (3.22)Из выражений (3.22) следует:
множитель перед синусом (косинусом) возрастает с течением времени и может стать сколь угодно большой величиной;
1) вынужденные колебания при резонансе отстают по фазе от возмущающей силы на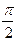 
.График расстояний при резонансе представляет собой синусоидальную кривую (рис. 3.3), ограниченную прямыми 
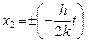, так как 
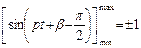.Полное решение уравнения следующее: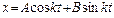 
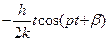, или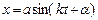 
,
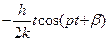где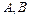 
(
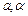) находятся из начальных условий.Член 
, содержащий сомножителем время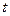 
, называется вековым членом решения.
Вопрос 16 Относительное движение материальной точки
Перейдем к изучению относительного движения точки, то есть ее движения по отношению к неинерциальным системам отсчета, движущимся произвольно относительно инерциальной системы.
Различие абсолютного и относительного движения определяется тем, что соответствующие им ускорения различны и связаны между собой теоремой Кориолиса
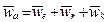. Отсюда следует различие остальных кинематических характеристик движения точки (траекторий, скоростей).
Пользуясь вторым законом Ньютона, выведем дифференциальные уравнения относительного движения МТ.
Пусть материальная точка М массой m движется в подвижной системе отсчета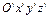 
, движущейся произвольно относительно неподвижной системы 
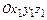(рис. 4.1). Положение точки в системе 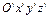определяется радиусом-вектором 
.
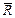Обозначим равнодействующую всех сил, непосредственно приложенных к МТ, через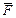 
, тогда
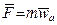,где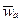 
– абсолютное ускорение точки (относительно неподвижной системы 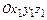).Умножим левую и правую части выражения (4.1) на массу 
: 
.
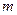Очевидно, что относительное движение определяется тремя силами: равнодействующей непосредственно приложенных к МТ сил и двумя дополнительными, которые наблюдаются только относительно подвижной системы отсчета.
Одной из этих сил является переносная сила инерции
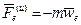. Она направлена противоположно переносному ускорению точки и численно равна произведению массы на его величину.
Вторая сила называется кориолисовой силой инерции
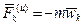. (4.4)
Она направлена противоположно ускорению Кориолиса и численно равна произведению массы на его величину.
Следовательно,
, 
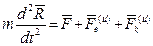.Это соотношение выражает динамическую теорему Кориолиса: относительное движение МТ происходит под действием не только непосредственно приложенной силы 
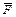, но и переносной силы инерции 
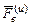и силы инерции Кориолиса 
.
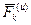Дифференциальные уравнения относительного движения МТ в проекциях подвижные на оси имеют вид
,
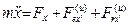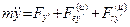, (4.6)
.
Предположим, что переносное движение подвижной системы координат является поступательным, то есть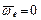 
, следовательно, равны нулю кориолисовы ускорение и сила инерции:
, 
.
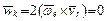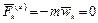Тогда
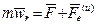, (4.7)
то есть относительное движение определяется действием непосредственно приложенных сил и переносной силы инерции.
Вопрос 17 КОЛИЧЕСТВО ДВИЖЕНИЯ
Date: 2015-09-03; view: 380; Нарушение авторских прав