
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проекции силы на оси
|
|
Материальная точка под действием нескольких сил получает ускорение, равное геометрической сумме тех ускорений, которые она получает от каждой силы, действующей отдельно, независимо от других.
Иначе, система сил, приложенных к одной МТ, динамически эквивалентна одной равнодействующей силе, равной главному вектору системы сил.
Пусть на МТ массой 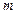 действуют силы
действуют силы 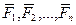 , сообщая ей ускорение
, сообщая ей ускорение 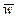 . При этом каждая из сил сообщает три ускорения
. При этом каждая из сил сообщает три ускорения 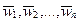 . Ускорение при действии нескольких сил является векторной суммой ускорений, созданных отдельными силами, то есть
. Ускорение при действии нескольких сил является векторной суммой ускорений, созданных отдельными силами, то есть
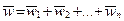 . (1.4)
. (1.4)
Умножим обе части этого выражения на 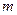
 , (1.5)
, (1.5)
где 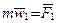 ,
, 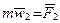 , …,
, …, 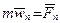 .
.
Тогда
 ,
,
следовательно,
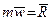 , (1.6)
, (1.6)
где 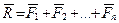 .
.
Получено основное уравнение динамики для случая одновременного действия нескольких сил. Под силой 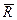 подразумевается равнодействующая всех сил, действующих на МТ.
подразумевается равнодействующая всех сил, действующих на МТ.
Вопрос 7 1-я задача Динамики.
Зная массу МТ и закон ее движения, требуется найти действующую на точку силу.
Известны законы движения вдоль координатных осей
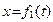 ,
, 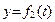 ,
, 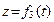 . (1.11)
. (1.11)
Проекции силы на оси
 ,
,
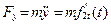 , (1.12)
, (1.12)
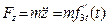 .
.
Следовательно, модуль вектора силы
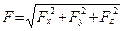 . (1.13)
. (1.13)
Направляющие косинусы
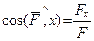 ,
, 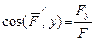 ,
,  . (1.14)
. (1.14)
Заметим, что реакции связей входят как составляющие в силу 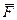 .
.
Вопрос 8 2-я задача динамики.
По заданной массе и действующей на МТ силе требуется определить закон движения точки.
Напишем выражение ускорения
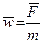 . (1.15)
. (1.15)
Дважды интегрируя по времени, находим закон движения точки вдоль траектории 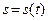 .
.
Date: 2015-09-03; view: 335; Нарушение авторских прав