Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вычисление кинетической энергии твердого тела в различных случаях его движения
|
|
Поступательное движение тела. Скорости всех точек тела равны между собой, следовательно,
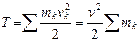, где 
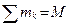– масса тела,тогда 
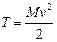, то есть кинетическая энергия поступательно движущегося тела равна половине произведения массы М на квадрат его скорости 
. При поступательном движении тела кинетическая энергия вычисляется так же, как и для одной точки, у которой масса равна массе всего тела. По этой формуле находится кинетическая энергия любой системы, движущейся так, что модули скоростей всех её точек одинаковы.
Вращение тела вокруг неподвижной оси (рис. 8.3). Скорость любой точки определяется по формул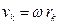е 
, где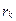 
– кратчайшее расстояние от точки до оси вращения, 
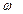– угловая скорость вращения тела. 
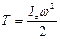, то есть кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции точки относительно этой оси на квадрат его угловой скорости.
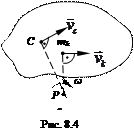
Плоско-параллельное движение тела (рис. 8.4). Кинетическая энергия вычисляется в соответствии с теоремой Кёнига. Покажем сечение тела плоскостью, проходящее через центр масс С и параллельное данной неподвижной плоскости.
Пусть известны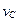 
и 
. Тело в данное мгновение вращается вокруг мгновенного центра скоростей (МЦС), положение которого определяется отрезком СР, повернутым перпендикулярно к 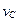и направленным в сторону вращения 
: 
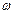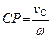.Кинетическая энергия тела 
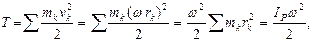где 
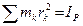– момент инерции тела относительно оси, перпендикулярной к плоскости сечения, проходящей через МЦС и являющейся мгновенной осью вращения.
Пользоваться этой формулой неудобно, так как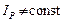 
. Преобразуем момент инерции по формуле Штейнера-Гюйгенса: 
, где 
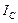– момент инерции тела относительно центральной оси, параллельной мгновенной оси вращения.Тогда 
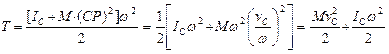. Окончательно имеем 
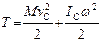, (8.11)
то есть кинетическая энергия тела при плоско-параллельном движении равна сумме кинетических энергий тела в переносном поступательном движении со скоростью центра масс и вращательного движения вокруг центральной оси, перпендикулярной плоскости движения.
Вопрос 30 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Для k -й точки системы применим теорему об изменении кинетической энергии МТ 
, где 
– кинетическая энергия точки в конце и начале некоторого перемещения системы соответственно,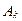 
– работа на том же перемещении равнодействующей всех сил, действующих на данную точку.
Написав аналогичные соотношения для каждой точки системы и сложив их почленно, получим
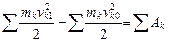,где 
, 
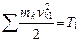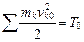– кинетическая энергия механической системы в конце и начале данного ее перемещения.
Следовательно, с учетом работ внешних и внутренних сил имеем
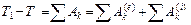, (8.13)
то есть изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на этом перемещении.
Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил равна нулю
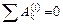,Следовательно, 
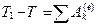, (8.14)
то есть изменение кинетической энергии твердого тела при каком-либо перемещении равно сумме работ всех внешних сил, действующих на тело, на соответствующих перемещениях точек при его перемещении.
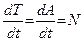, то есть производная по времени от кинетической энергии равна мощности.
Для членов, входящих в выражение кинетической энергии и относящихся к поступательно движущимся телам,
.
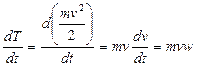Мощность
.
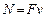Приравнивая правые части этих выражений, получим
,
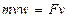откуда находим ускорение
.
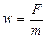Аналогично для членов, относящихся к вращающимся телам,
.
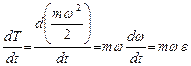Мощность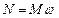 
.
Приравниваем правые части между собой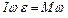 
,откуда угловое ускорение 
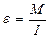. (8.17)
Очевидно, в том и другом случае с исключением скоростей происходит переход к ускорениям, которые легко находятся.
Вопрос 31 КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
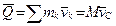, (9.1)
то есть количество движения механической системы равно количеству движения ее центра масс в предположении, что в нем сосредоточена вся масса системы (рис. 9.1).
Date: 2015-09-03; view: 4337; Нарушение авторских прав