Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Работа силы тяжести
|
|
Силу тяжести G считаем постоянной, направленной вертикально вниз (рис. 6.3). Ее проекции на координатные оси Gх = 0, Gy = 0, Gz = – mg.
Вычислим работу силы тяжести при перемещении из точки М 0 в точку М 1:
(6.9)
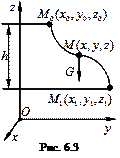Обозначим высоту опускания 
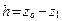. Тогда
А = mgh,
то есть работа силы тяжести равна произведению силы тяжести на разность горизонтальных уровней в начале и конце перемещения.
В общем случае A = ± mgh (при опускании "+", при поднятии "-"). Работа на замкнутом перемещении равна нулю.
Вопрос 21 Работа линейной силы упругости
Линейной силой упругости (линейной восстанавливающей силой) называется сила, действующая по закону Гука:
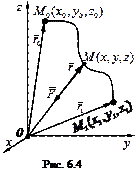
, (6.10)
где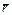 
– радиус-вектор точки М (рис. 6.4), его модуль – расстояние от рассматриваемой точки до точки статического равновесия, то есть точки, в которой эта сила равна нулю; с – постоянная величина.
Выбрав начало координат в положении статического равновесия, имеем
Fx = – cx, Fy = – cy, Fz = – cz.
Тогда
,
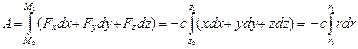так как xdx + ydy + zdz = rdr, где r 2 = x 2 + y 2 + z 2.
Выполнив интегрирование, получим
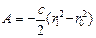. Если точка М 0 совпадает с точкой статического равновесия, то работа силы упругости на этом перемещении 
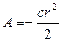, где r – кратчайшее расстояние от рассматриваемой точки 
до точки О.
Обозначим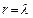 
, тогда 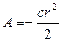, то есть работа линейной силы упругости на перемещении из положения статического равновесия всегда отрицательна и равна половине произведения коэффициента жесткости на квадрат перемещения из положения статического равновесия. Отсюда следует, что работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю.
Вопрос 22 МОЩНОСТЬ
Мощность, или работоспособность, какого-либо источника оценивается той работой, которую он может совершить за единицу времени.
По определению,
.
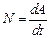Учитывая формулу для определения элементарной работы (6.3), мощность можно представить в виде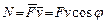 
, то есть мощность равна скалярному произведению силы на скорость точки.
Из этой формулы видно, что от источника с заданной мощностью можно получить бóльшую силу при меньшей скорости («золотое правило механики»). Например, локомотив трогает с места железнодорожный состав при малой скорости, развивая значительно бóльшую силу тяги, чем при движении.
Размерность мощности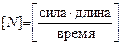 
.
В технической системе единиц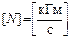 
, в системе CИ 
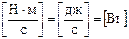, 1 кВт = 1000 Вт.
В инженерной практике существует единица мощности «лошадиная сила» (л.с.):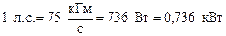 
, 
Вопрос 23 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
Кинетической энергией МТ (ее «живой силой») называется половина произведения ее массы на квадрат скорости:
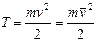. Размерность кинетической энергии в системе СИ 
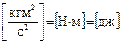, то есть такая же, как и у работы. Напишем основное уравнение динамики для МТ:
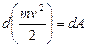. (6.13)
Это теорема об изменении кинетической энергии МТ в дифференциальной форме: дифференциал кинетической энергии МТ равен элементарной работе силы, действующей на нее.
Разделив обе части на dt, получим
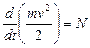, (6.14)
то есть производная по времени от кинетической энергии МТ равна мощности, подводимой к ней.
Интегрируя обе части формулы (6.3) от точки М 0 до точки М 1, получим теорему об изменении кинетической энергии МТ в конечной форме
, (6.15)
то есть изменение кинетической энергии МТ на каком-либо перемещении равно работе силы, действующей на МТ, на том же перемещении.
Вопрос 24 Внешние и внутренние силы
Механической системой (в дальнейшем просто системой) называется совокупность МТ, взаимодействующих между собой. Эти МТ находятся во взаимосвязи, и движение и положение каждой из них определяется движением и положением всех остальных МТ.
Система считается свободной, если движение ее МТ не ограничено какими-либо связями, и несвободной, если такие связи имеются.
Системы делятся на изменяемые и неизменяемые. Неизменяемые системы те, в которых расстояния между любыми двумя точками остаются постоянными при движении (например, абсолютно твердое тело). Если эти расстояния изменяются, то система называется изменяемой (например, деформируемое тело).В статике силы разделялись на активные и реакции связей. В динамике силы делят на внешние и внутренние.
Внешними силами механической системы называются силы взаимодействия точек этой системы с телами и точками, не входящими в состав механической системы (обозначаются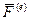 
).
Внутренними силами механической системы называются силы взаимодействия между точками системы (обозначаются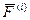 
).
Рассматривая попарно силы взаимодействия всех МТ системы, можно сделать выводы.
1. Главный вектор внутренних сил системы и его проекции на координатные оси (алгебраические суммы проекций этих сил на оси) равны нулю (рис. 7.1).
2. Главный момент внутренних сил относительно любого центра и главный момент (алгебраическая сумма моментов) этих сил относительно любой оси равны нулю. Из рис. 7.1 видно, что
. (7.3)
Обе силы имеют одинаковые модули и противоположные направления.
.
Вопрос 25 МОМЕНТЫ ИНЕРЦИИ тел
При решении ряда задач определяются динамические величины, выражающиеся через суммы произведений масс точек системы на квадраты их расстояний до оси, точки или плоскости. Эти величины характеризуют распределение масс системы относительно них. Они называются моментами инерции относительно оси, точки, плоскости.
Относительно полюса О
Относительно осей
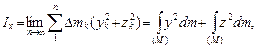
Относительно плоскостей
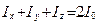, то есть сумма моментов инерции относительно координатных осей равна двум моментам инерции относительно полюса (начала системы координат); 
,
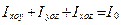то есть сумма моментов инерции относительно координатных плоскостей равна моменту инерции относительно полюса.
Размерность момента инерции [ I ]=[ 
]. В системе СИ 
.Нередко при расчетах используется понятие радиуса инерции. Радиусом инерции относительно оси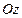 
называется линейная величина, определяемая из соотношения
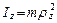,откуда 
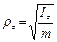, где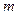 
– масса тела.
Радиус инерции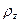 
равен расстоянию от оси 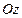той точки, в которой надо сосредоточить массу тела, чтобы ее момент инерции относительно этой оси был равен моменту инерции тела.
Вопрос 26. ТЕОРЕМА ШТЕЙНЕРА-ГЮЙГЕНСА
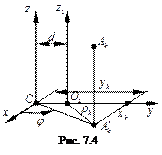
Момент инерции системы относительно какой-либо оси равен моменту инерции системы относительно оси, проходящей через центр масс системы параллельно ей, плюс произведение массы системы на квадрат расстояния между осями (рис. 7.4).
Напишем
,
,
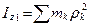где по теореме косинусов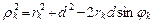 
.
Тогда
,
где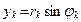 
, 
, 
.
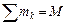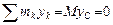Следовательно,
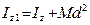. (7.15)
Из этой формулы видно, что для совокупности параллельных осей момент инерции относительно центральной оси (проходящий через центр масс) является наименьшим.
ВОПРОС 27. МОМЕНТЫ ИНЕРЦИИ ОДНОРОДНЫХ ТЕЛ
Стержень.
Масса стержня М, длина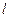 
(рис. 7.5).
Относительно оси, проходящей через конец стержня,
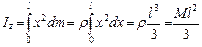, где 
– погонная масса стержня.Центральный момент инерции находим по теореме Штейнера-Гюйгенса 
, 
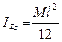. (7.17)
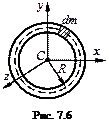
Кольцо.
Масса распределена по ободу (рис. 7.6). Центральный момент инерции относительно оси z, перпендикулярной к плоскости кольца,
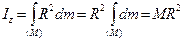. (7.18)
В соответствии с равенством (7.12)
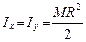. (7.19)
Круглый диск
Центральный момент инерции относительно оси z, перпендикулярной к плоскости диска (рис. 7.7),
,
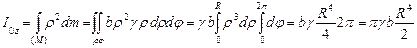где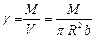 
, V – объем диск. Тогда 
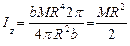. Другие осевые моменты инерции 
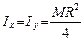. (7.21)
Шар
Момент инерции относительно центра (рис. 7.8):
,
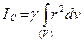где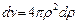 
.
Тогда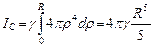 
,
где плотность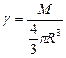 
.Следовательно, 
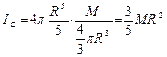. На основании равенства (7.12) осевые моменты инерции
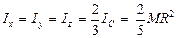. (7.23)
ВОПРОС 28. РАБОТА И МОЩНОСТЬ СИЛ,ПРИЛОЖЕННЫХ
Date: 2015-09-03; view: 1139; Нарушение авторских прав