Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении количества движения системы
|
|
Напишем теорему об изменении количества движения k -й материальной точки, выделив внешние и внутренние силы:
, где 
и 
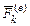– равнодействующие внешних и внутренних сил, действующих на МТ.
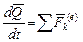. Получена теорема об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме внешних сил, действующих на систему.
Спроектируем соотношение (9.4) на координатные оси:
, 
, 
,
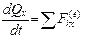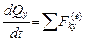то есть производная по времени от проекции количества движения системы на какую-либо ось равна алгебраической сумме проекций всех внешних сил, действующих на систему.
Умножив обе части соотношения (9.4) на dt, получим
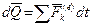, (9.5)
то есть дифференциал количества движения системы равен векторной сумме элементарных импульсов внешних сил, действующих на систему.
В проекциях на координатные оси
, 
, 
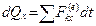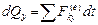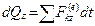. (9.6)
Беря интеграл от обеих частей равенства (9.5), имеем
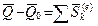. (9.7)
Получена теорема об изменении количества движения механической системы в конечной форме: изменение количества движения системы за какой-то промежуток времени равно векторной сумме импульсов всех внешних сил, действующих на систему, за то же время.
В проекциях на координатные оси
, 
, 
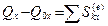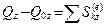. (9.8)
Отметим следующее:
1) внутренние силы не входят в теорему об изменении количества движения системы и, следовательно, не влияют на его величину;
2) при некоторых условиях для внешних сил можно получить первые интегралы системы дифференциальных уравнений движения системы.
Следствие. Закон сохранения количества движения системы.
Положим, что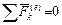 
, тогда 
.
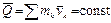Если в течение некоторого времени главный вектор внешних сил, действующих на систему, равен нулю, то количество движения системы за это время остается постоянным.
По аналогии для проекций на координатные оси, если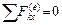 
, то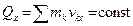 
.
Если в течение некоторого времени алгебраическая сумма проекций на какую-либо ось внешних сил, действующих на систему, остается равной нулю, то проекция на ту же ось количества движения системы за это время остается постоянной величиной.
Вопрос 32 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
На основании выражения (9.4), с учетом того, что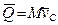 
, имеем
.
Здесь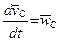 
– ускорение центра масс, поэтому
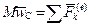. (9.9)
Получена теорема о движении центра масс системы: центр масс системы движется так же, как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все внешние силы, приложенные к системе.
Аналогично для проекций на координатные оси
, 
, 
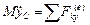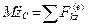, (9.10)
где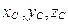 
– координаты центра масс.
Date: 2015-09-03; view: 490; Нарушение авторских прав