Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Материальной точки
В зависимости от характера деформаций упругого элемента различаются продольные, поперечные, изгибные, крутильные колебания.Это определено наличием силовых факторов, которые при отклонении системы от положения устойчивого равновесия стремятся вернуть ее в исходное положение. Предполагается, что величина каждого из этих силовых факторов прямо пропорциональна величине деформации упругого элемента, который работает в зоне линейной упругости, то есть в пределах закона Гука.
Удобно в качестве упругого элемента принять пружину, работающую на продольное растяжение-сжатие. Ее упругая сила определяется выражением
,
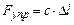где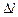 
– деформация, 
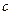– коэффициент жесткости пружины. Размерность 
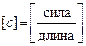, в системе СИ 
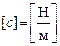. Он численно равен значению силы, деформирующей пружину на единицу длины.
На графике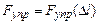 
(рис. 2.3) коэффициент жесткости выражается тангенсом угла наклона прямой к оси 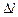, т.е. 
.
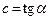Существуют два основных вида соединения пружин: параллельное и последовательное.
При параллельном соединении (рис. 2.4) две пружины можно заменить одной пружиной с эквивалентным коэффициентом жесткости:
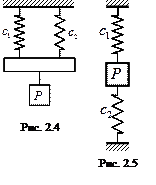
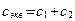. (2.22)
Параллельным также является соединение, показанное на рис. 2.5.
При последовательном соединении (рис. 2.6) справедливо равенство
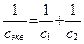, или 
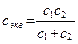. (2.23) 
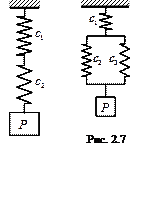Формулы (2.22), (2.23) аналогичны соотношениям, используемым при расчетах конденсаторных цепей в электротехнике. Это обстоятельство используется при электрическом моделировании механических явлений.
|
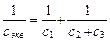, то есть 
. (2.24)
Колебания делятся на свободные, затухающие, вынужденные.
Вертикально подвешенная пружина имеет начальную длину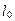 
(рис. 2.8, а). При отсутствии нагрузки упругая сила пружины равна нулю.
При подвешивании тела (рис. 2.8, б) весом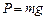 
упругая сила пружины равна силе тяжести тела 
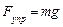. Пружина растянута на величину статической деформации 
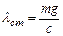. Это положение тела удобно принимать за начало отсчета перемещений 
.
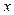Вопрос 11 СВОБОДНЫЕ КОЛЕБАНИЯ.Частота,амплитуда,период колебаний.
Дифференциальное уравнение движения МТ
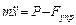, где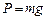 
, 
.
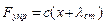гармоническое колебательное движение (рис. 2.9).
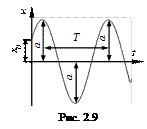Колебания точки, происходящие под действием только восстанавливающей силы, называются свободными, или собственными.
Период колебаний
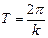, где k – циклическая (круговая) частота колебаний:
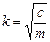. Следовательно, 
.
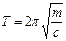Частота и период свободных колебаний зависят от массы точки и коэффициента с. Величина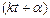 
– фаза колебаний, 
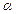– начальная фаза колебаний, а – амплитуда свободных колебаний.
.
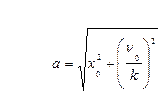Вопрос 12 ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
При затухающих колебаниях, кроме силы тяжести и упругой силы пружины, на МТ массой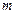 
действует сила сопротивления среды 
.
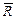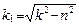– частота затухающих колебаний.
Общее решение уравнения
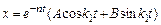, где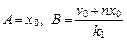 
– постоянные интегрирования, найденные из начальных условий. 
. 
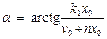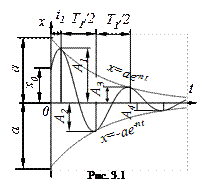Эти колебания называются затухающими, так как амплитуда 
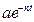убывает с течением времени. Их график – затухающая синусоида, ограниченная двумя симметричными кривым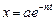и 
и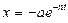 
, так как 
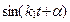изменяется пределах от 
до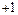 
(рис. 3.1).Промежуток времени между двумя соседними крайними (нижними или верхними) положениями точки называется периодом затухающих колебаний
. 
.
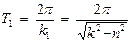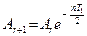Число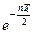 
называется декрементом колебаний, а его натуральный логарифм, величина 
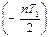, – логарифмическим декрементом колебаний.
Очевидно, последовательные значения амплитуд затухающих колебаний представляют собой убывающую геометрическую прогрессию, знаменатель которой равен декременту колебаний.
Вопрос 13 АПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ
Корни характеристического уравнения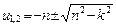 
действительные и меньше нуля.Решение уравнения 
.
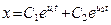Так как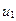 
< 
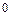и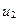 
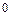< , то, независимо от значений 
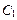и 
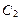, при 
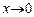. Это означает, что с течением времени точка неограниченно приближается к равновесному положению.
Представив корни характеристического уравнения в виде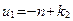 
, 
, получим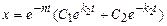 
.
Определим моменты, когда точка занимает крайние положения. В них ее скорость равна нулю:
.
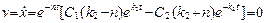Обозначим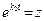 
, тогда 
.
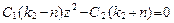Момент времени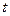 
имеет действительное положительное значение только при 
> 
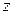, а этих значений в зависимости от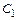 
и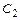 
имеется или одно, или совсем не имеется, что относится и к случаю 
.
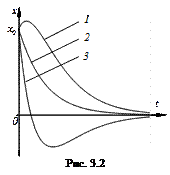На рис. 3.2 показаны кривые возможных движений точки в зависимости от начальных условий при 
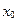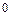> .Кривая 1 соответствует начальной скорости, направленной в положительную сторону оси 
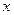;кривая 2 – относительно небольшой начальной скорости, направленной в отрицательную сторону оси 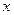; кривая 3 – большой начальной скорости, направленной в отрицательную сторону оси .
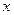При 
корни характеристического уравнения равны между собой (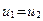
), и решение дифференциального уравнения:
.
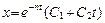Характер движения тот же, что и при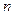 
> 
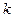. В случае большого сопротивления (
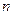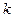>> ) колебаний нет. Это движение называется апериодическим затухающим.
Вопрос 14 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Date: 2015-09-03; view: 306; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |