Зависимость амплитуд от времени

ВРЕМЯ И ПРОСТРАНСТВО В КВАНТОВОЙ МЕХАНИКЕ

Ранее мы уже отмечали, что амплитуда события закономерно зависит от локализации этого события во времени и в пространстве. Эти закономерности можно описать относительно простыми уравнениями, используя понятия вектора (или функции) состояния и оператора.

ЗАВИСИМОСТЬ АМПЛИТУД ОТ ВРЕМЕНИ

Представим себе устройство ("прибор"), в котором с частицами ничего не происходит: частица предоставлена самой себе и подвергается только действию времени. Влияние времени на состояние частицы можно исследовать стандартным способом — с помощью некоторого спектрального анализатора (А). Для этого следует проанализировать приготовленное состояние частиц в разные моменты времени, например t ₁и t ₂. В качестве результата анализа будут выступать два вектора состояния:

| Y ñ t ₁ = A ₁ | 1 ñ + A ₂ | 2 ñ +.... + A_n | n ñ

| Y ñ t ₂ = A' ₁ | 1 ñ + A' ₂ | 2 ñ +.... + A'_n | n ñ

В общем случае результат анализа (т.е. набор чисел-координат A_i) зависит от момента времени, в который производится анализ, т.е. с течением времени состояние частицы изменяется. Для описания такой эволюции во времени удобно представить состояние в виде вектора, координаты которого закономерно зависят от времени:

| Y ñ t = A ₁(t) | 1 ñ + A ₂(t) | 2 ñ +.... + A_n (t) | n ñ

Зная, как выглядят функции A_i (t), можно вычислить числовые значения координат вектора состояния в произвольный момент времени t. Подчеркнем, что при таком подходе зависимость от времени заключена в координатах вектора, тогда как базисные состояния от времени никак не зависят. Такой способ введения времени в квантово-механические уравнения называется представлением Шредингера.

Существуют и другие способы решения той же проблемы. Так, в представлении Гейзенберга время вводится в базисные состояния, тогда как координаты вектора состояния предполагаются постоянными:

| Y ñ t = A ₁ | 1 (t) ñ + A ₂ | 2 (t) ñ +.... + A_n | n (t) ñ

Наиболее общим вариантом является представление Дирака, в котором временная зависимость разделяется определенным способом между координатами и базисными состояниями:

| Y ñ t = A ₁ (t) | 1 (t) ñ + A ₂ (t) | 2 (t) ñ +.... + A_n (t) | n (t) ñ

Рассмотрим эволюцию состояния системы за промежуток времени между двумя измерениями: D t = t ₂ – t ₁, в течение которого совершается переход | Y ñ t ₁® | Y ñ t ₂. Этот переход удобно описать с помощью специального оператора эволюции U _{D t}.

| Y ñ t ₂ = U _{D t} | Y ñ t ₁

Это векторно-операторное уравнение можно записать в координатном представлении, например через вектор-столбцы и квадратную матрицу:

В соответствии с правилами линейной алгебры, мы можем заменить это уравнение эквивалентной системой из n уравнений вида:

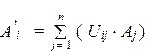
которые позволяют вычислять координаты второго вектора из известных координат первого и матричных элементов оператора эволюции.

Достаточно очевидно, что каждому отрезку времени соответствует свой оператор эволюции, т.е. для описания произвольных процессов эволюции потребуется бесконечно много таких операторов. В действительности, однако, операторы эволюции тесно связаны между собой. Рассмотрим два последовательных промежутка времени, которым соответствуют операторы эволюции U (t ₂, t ₁) и U (t ₃, t ₂). Сумма двух, следующих друг за другом, промежутков времени (D t ₂₁ = t ₂ – t ₁ и D t ₃₂ = t ₃ – t ₂) может, очевидно, рассматриваться как один большой промежуток (D t ₃₁ = t ₃ – t ₁), которому соответствует свой оператор эволюции U (t ₃, t ₁):

Тогда между тремя перечисленными операторами существует простое соотношение:

U (t ₃, t ₁) = U (t ₃, t ₂) × U (t ₂, t ₁)

Отсюда можно заключить, что операторы эволюции для более крупных промежутков времени можно строить в виде произведений операторов для более мелких промежутков. Это позволяет выбрать некоторый стандартный промежуток времени (достаточно малый), найти для него оператор эволюции и из него строить все остальные. Наиболее удобно в качестве такого стандартного промежутка взять бесконечно малый интервал (dt). Соответствующий стандартный оператор U _dt называется оператором бесконечно-малого сдвига во времени (или "инфинитезимальным" оператором эволюции).

Рассмотрим вид матричных элементов оператора эволюции, который осуществляет сдвиг от начального момента времени t ₁ = 0 к текущему моменту t ₁ = t. Очевидно, что матричные элементы будут функциями времени: U_ij = j(t). Любую из этих функций можно разложить в степенной ряд (ряд Тейлора):

j(t) = j(0) + С ₁(t) + C ₂(t)² + • • •

где коэффициенты С ₁, С ₂ и т.д. пропорциональны производным первой, второй и т.д. степени.

Для бесконечно малого сдвига во времени степенями величины dt, начиная с 2, можно пренебречь. Поэтому зависимость U_ij (t) может быть представлена более простым образом:

Очевидно, что при нулевой величине сдвига (t = 0) конечный вектор не будет отличаться от исходного, т.е. A'_i = A_i. Следовательно, матричные элементы U_ij (0) должны образовывать единичную матрицу (символ Кронекера или дельта-символ — d _ij):

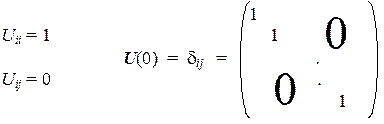
С учетом этого результата выражение для матричного элемента приобретет вид:

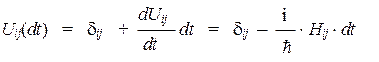
(переименование коэффициента разложения dU_ij / dt ® –(i/h) H_ij осуществляется по соображениям размерности). Подставив полученное выражение в исходную систему уравнений, получим:

A'_i = å [d _ij – (i/h) H_ij dt ] A_j = åd _ij A _j – (i/h)å(H_ij A_j) dt =

= A_i – (i/h)å(H_ij A_j) dt

Отсюда легко получить следующую форму системы уравнений:

которую удобно переписать в матричном виде

или в операторном виде с использованием векторов состояния:

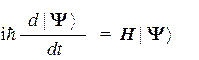
или волновых функций:

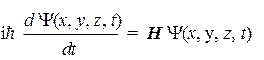
Это уравнение называется уравнением Шредингера, а входящий в него оператор Н — оператором Гамильтона (или гамильтонианом).

Таким образом, можно узнать, насколько изменилось некоторое начальное состояние за время dt, располагая только оператором Гамильтона:

Y(t + dt) = Y(t) + d Y = Y(t) – (i / h) [ H • Y(t)] dt

Последовательно проводя такую операцию сдвига во времени (+ dt или – dt), можно легко предсказать все будущие и прошлые состояния системы.

Следует подчеркнуть, что гамильтониан зависит от внешних условий, в которых находится система — если эти условия изменить, то изменится и характер эволюции системы во времени.

Рассмотрим некоторые свойства оператора Гамильтона.

Как у всякого квантово-механического оператора, у гамильтониана имеется набор собственных векторов (функций) и собственных значений:

которые удовлетворяют уравнению на собственные значения:

H | h _i ñ = l _i × | h _i ñ и H j _i = l_i × j _i

Возьмем одну из собственных функций гамильтониана и подставим ее в уравнение Шредингера:

В этом случае операторное уравнение превращается в простое дифференциальное уравнение с разделяющимися переменными, которое может быть легко проинтегрировано:

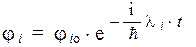
Заметим, что комбинация величин, стоящая в показателе экспоненты:

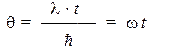
представляет собой фазу комплексной экспоненты, т.е. безразмерное число. Отсюда можно заключить, что размерность собственного значения гамильтониана выражается в [Дж]. Поэтому, собственные значения оператора Гамильтона представляют собой допустимые значения квантовомеханической наблюдаемой, называемой, по аналогии с классической механикой, энергией (e): l _i = e _i. Отношение w _i = e _i /h (с размерностью [с^–1]) называется частотой, которая, в сущности, также представляет собой энергию, но измеренную в единицах h.

Теперь собственные функции гамильтониана можно записать так:

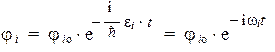
Очевидно, что каждой собственной функции гамильтониана соответствует своя строго определенная энергия (и частота). Этот признак является характерным, и любое квантово-механическое состояние со строго определенной энергией является одновременно и собственным для некоторого оператора Гамильтона.

Из приведенных формул видно, что собственные функции гамильтониана зависят от времени, причем временная зависимость всегда имеет строго определенный вид: фаза комплексной экспоненты прямо пропорциональна времени: q = w t.

Располагая этой информацией, можно описать зависимость от времени для любой волновой функции. Для этого достаточно воспользоваться принципом суперпозиции. Набор собственных функций любого оператора образует базис. Поэтому можно произвольную функцию представить в виде линейной комбинации собственных функций гамильтониана:

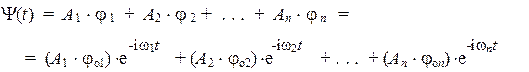
Легко видеть, что несобственным функциям всегда соответствует несколько частот, тогда как каждой собственной функции соответствует единственная и строго определенная частота. По этой причине собственные состояния гамильтониана иногда называют монохроматическими.

Date: 2015-09-03; view: 765; Нарушение авторских прав