
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общая схема исследования функции
|
|
1. Найти область определения функции, исследовать ее поведение на границах области определения.
2. Найти точки разрыва и установить их характер с помощью односторонних пределов.
3. Исследовать периодичность, четность (нечетность), найти точки пересечения графика с осями координат.
4. Найти интервалы монотонности и экстремумы функции.
5. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
6. Найти асимптоты графика.
7. Построить график, используя результаты исследования.
Задача 4. Провести полное исследование и построить график функции 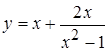 .
.
1. Найдем область определения 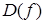 . из условия
. из условия  ,
, 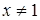 ,
,  , следовательно,
, следовательно,
2.  ,
,  – точки разрыва. Найдем односторонние пределы:
– точки разрыва. Найдем односторонние пределы:
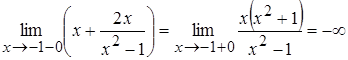 ,
,  ,
,
 ,
,  .
.
Отсюда следует, что  и
и  – точки разрыва второго рода, и
– точки разрыва второго рода, и 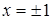 – вертикальные асимптоты.
– вертикальные асимптоты.
3. Для установления симметрии графика функции
найдем 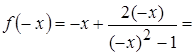
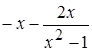 = –
= – 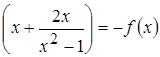 , это означает, что
, это означает, что  – нечетная функция, и ее график симметричен относительно начала координат. Достаточно провести ее исследование для
– нечетная функция, и ее график симметричен относительно начала координат. Достаточно провести ее исследование для  . Очевидно, что функция не является периодической. Точка О (0,0) является единственной точкой пересечения с осями координат, т.к.
. Очевидно, что функция не является периодической. Точка О (0,0) является единственной точкой пересечения с осями координат, т.к. 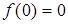 .
.
4. Первая производная:  ,
,
Критические точки найдем из условий 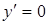 ,
, 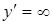 .
.
а)  ,
, 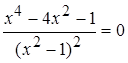 ,
, 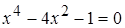 ,
,  .
.
Решая биквадратное уравнение, найдем  .
.
б)  ,
,  ,
,  ,
,  .
.
Таким образом, критические точки функции:  ,
, 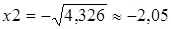 , а точки
, а точки  не входят в область определения, следовательно, не являются критическими точками. Проверим критические точки на экстремум по первому признаку.
не входят в область определения, следовательно, не являются критическими точками. Проверим критические точки на экстремум по первому признаку.
 , при
, при  ,
, 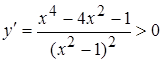 , при
, при 
Так как производная меняет знак при переходе через критическую точку, то в точке 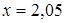 функция имеет минимум. Составим таблицу.
функция имеет минимум. Составим таблицу.
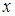
| (0, 1) | (1; 2.05) | 2,05 | (2,05,  ) )
| ||

| 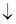
| не сущ. | 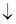
| (min) 3,4 | 
| |

| – | не сущ. | – | + |
5. Найдем 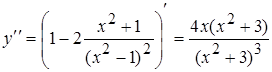 . Критические
. Критические
точки второго рода найдем из условия 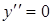 ,
,  ,
,  ; при
; при  ,откуда
,откуда 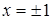 . Так как
. Так как 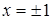 не входят в область определения функции, то
не входят в область определения функции, то  единственная критическая точка. Проверим знак второй производной при переходе через точку
единственная критическая точка. Проверим знак второй производной при переходе через точку 
 при
при  ,
,
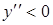 при
при 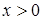 .
.  меняет знак с «+» на «–», значит,
меняет знак с «+» на «–», значит,  – точка перегиба, и график меняет вогнутость на выпуклость при переходе через критическую точку. Итак, в (0, 1) функция выпукла, а в
– точка перегиба, и график меняет вогнутость на выпуклость при переходе через критическую точку. Итак, в (0, 1) функция выпукла, а в  – вогнута.
– вогнута.
6. Найдем асимптоты. Наклонные асимптоты имеют вид: 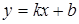 ;
;
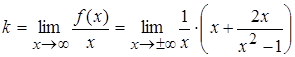 =
= 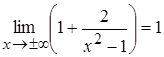 ,
,

 ,
,  ,
,
отсюда уравнение наклонной асимптоты  . Горизонтальные асимптоты отсутствуют, а вертикальные были найдены в п. 2.
. Горизонтальные асимптоты отсутствуют, а вертикальные были найдены в п. 2.
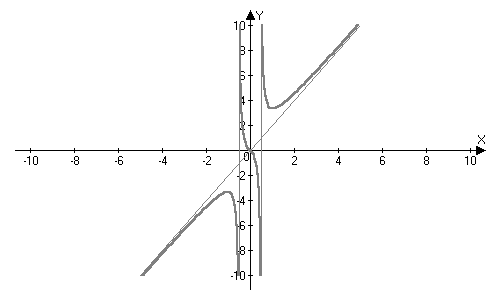
7. По результатам исследования построим график. Так как
функция нечетная, то можно построить график для 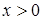 и отобразить его симметрично начала координат.
и отобразить его симметрично начала координат.
 |
Варианты контрольных заданий для контрольной работы № 2
Задания
1. Найти первую производную для указанных функций.
2. Функция задана параметрически. Найти 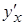 ,
,  .
.
3. Найти наибольшее и наименьшее значение функции на замкнутом отрезке.
4. Вычислить пределы, применив правило Лопиталя.
5. Исследовать функции по полной схеме и построить графики.
6. Вычислить приближенно значение выражения с помощью дифференциала.
Вариант 1
1. a)  , б)
, б) 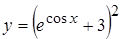 ,
,
в) 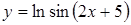 , г)
, г)  , д)
, д) 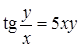 ;
;
2. 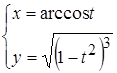 ; 3.
; 3.  ,
,  ;
;
4. а) 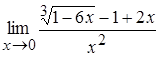 , б)
, б) 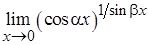 ;
;
5. а)  , б)
, б)  ; 6.
; 6.  .
.
Вариант 2
1. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
2.  3.
3. 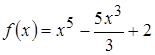 ,
, 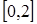 ;
;
4. а) 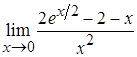 , б)
, б)  ;
;
5. а) 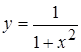 , б)
, б) 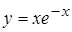 ; 6.
; 6. 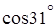 .
.
Вариант 3
1. а)  , б)
, б)  , в)
, в)  ,
,
г) 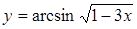 , д)
, д) 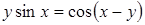 ;
;
2. 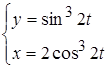 ; 3.
; 3. 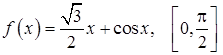 ;
;
4. а)  , б)
, б) 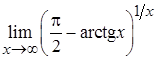 ;
;
5. а)  , б)
, б)  ; 6.
; 6.  .
.
Вариант 4
1. а) 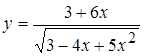 , б)
, б) 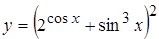 ,
,
в)  , г)
, г)  , д)
, д) 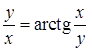 ;
;
2.  ; 3.
; 3. 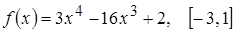 ;
;
4. а)  , б)
, б) 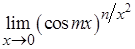 ;
;
5. а) 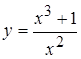 , б)
, б)  ; 6.
; 6. 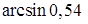 .
.
Вариант 5
1. а) 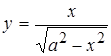 , б)
, б)  ,
,
в)  , г)
, г)  , д)
, д) 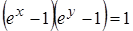 ;
;
2.  ; 3.
; 3.  ;
;
4. а)  , б)
, б)  ;
;
5. а)  , б)
, б) 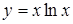 ; 6.
; 6. 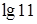 .
.
Вариант 6
1. а) 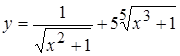 , б)
, б)  ,
,
в)  , г)
, г) 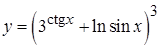 , д)
, д)  .
.
2. 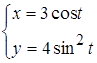 ; 3.
; 3. 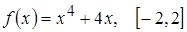 .
.
4. а)  , б)
, б)  ;
;
5. а) 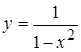 , б)
, б) 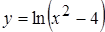 ; 6.
; 6.  .
.
Вариант 7
1. а) 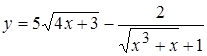 , б)
, б) 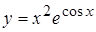 ,
,
в)  , г)
, г) 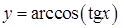 , д)
, д)  ;
;
2.  ; 3.
; 3. 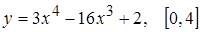 ;
;
4. а)  , б)
, б)  ;
;
5. а)  ; б)
; б)  ; 6.
; 6. 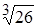 .
.
Вариант 8
1. а) 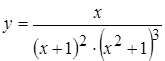 , б)
, б)  ,
,
в)  г)
г) 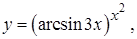
д) 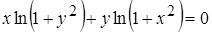 ;
;
2.  ; 3.
; 3.  ;
;
4. а)  , б)
, б) 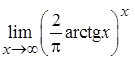 ,
,
5. а)  , б)
, б) 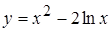 ; 6.
; 6. 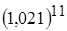 .
.
Вариант 9
1. а)  , б)
, б)  , в)
, в) 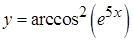 ,
,
г) 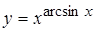 , д)
, д)  .
.
2.  ; 3.
; 3. 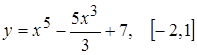 ;
;
4. а)  , б)
, б)  ;
;
5. а)  , б)
, б)  ; 6.
; 6. 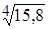 .
.
Вариант 10
1. а)  , б)
, б)  , в)
, в)  ,
,
г) 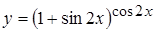 , д)
, д) 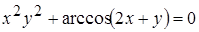 ;
;
2. 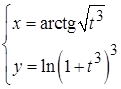 ; 3.
; 3.  ;
;
4. а) 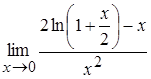 , б)
, б)  ;
;
5. а) 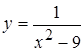 , б)
, б) 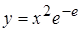 , 6.
, 6.  .
.
Вариант 11
1. а)  , б)
, б) 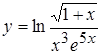 ,
,
в) 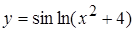 , г)
, г)  , д)
, д)  ;
;
2.  ; 3.
; 3. 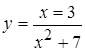 ,
,  ;
;
4. а)  , б)
, б)  ;
;
5. а)  , б)
, б) 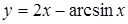 ; 6.
; 6. 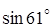 .
.
Вариант 12
1. а)  , б)
, б) 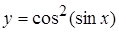 , в)
, в)  ,
,
г)  , д)
, д) 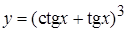 ,
,
2.  ; 3.
; 3.  ,
,  ;
;
4. а)  , б)
, б)  ;
;
5. а)  , б)
, б) 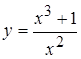 ; 6.
; 6.  .
.
Вариант 13
1. а) 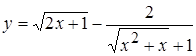 , б)
, б) 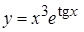 ,
,
в) 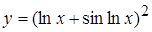 , г)
, г)  , д)
, д)  ;
;
2. 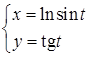 ; 3.
; 3. 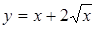 ,
,  ;
;
4. а)  , б)
, б)  ;
;
5. а) 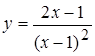 , б)
, б) 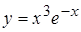 ; 6.
; 6. 
Вариант 14
1. а)  , б)
, б)  ,
,
в)  , г)
, г)  , д)
, д) 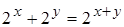 ;
;
2. 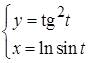 ; 3.
; 3. 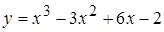 ,
,  ;
;
4. а)  , б)
, б)  ;
;
5. а) 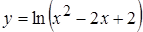 , б)
, б) 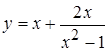 ; 6.
; 6. 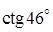 .
.
Вариант 15
1. а)  , б)
, б) 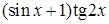 ,
,
в) 
 , г)
, г)  , д)
, д)  ;
;
2. 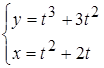 ; 3.
; 3. 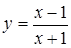 ,
,  ;
;
4. а) 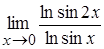 , б)
, б)  ;
;
5. а) 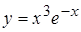 , б)
, б)  ; 6.
; 6.  .
.
Вариант 16
1. а)  , б)
, б)  , в)
, в) 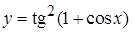 ,
,
г) 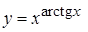 , д)
, д) 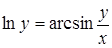 ;
;
2.  ; 3.
; 3. 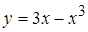 ,
, 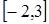 ;
;
4. а)  , б)
, б)  ;
;
5. а)  , б)
, б) 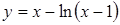 ; 6.
; 6. 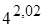 .
.
Вариант 17
1. а)  , б)
, б)  , в)
, в) 
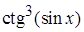 ,
,
г) 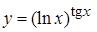 , д)
, д)  ;
;
2.  ; 3.
; 3.  ,
, 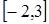 ;
;
4. а) 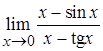 , б)
, б) 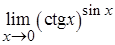 ;
;
5. а)  , б)
, б) 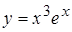 ; 6.
; 6. 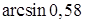 .
.
Вариант 18
1. а)  , б)
, б) 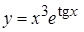 , в)
, в) 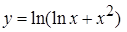 ,
,
г) 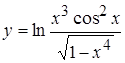 , д)
, д)  ;
;
2. 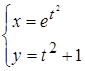 ; 3.
; 3.  ,
,  ;
;
4. а)  , б)
, б) 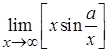 ;
;
5. а)  , б)
, б) 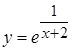 ; 6.
; 6.  .
.
Вариант 19
1. а)  , б)
, б)  , в)
, в) 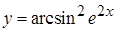 ,
,
г)  , д)
, д) 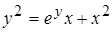 ;
;
2. 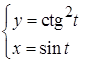 ; 3.
; 3. 
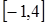 ;
;
4. а) 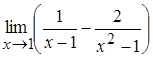 , б)
, б) 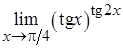 ;
;
5. а)  , б)
, б) 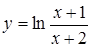 ; 6.
; 6. 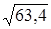 .
.
Вариант 20
1. а) 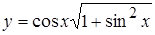 , б)
, б)  , в)
, в) 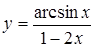 ,
,
г)  , д)
, д) 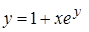 ;
;
2. 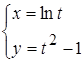 ; 3. а)
; 3. а)  , б)
, б) 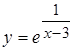 ;
;
4. а)  , б)
, б) 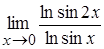 ;
;
5. а)  , б)
, б)  ; 6.
; 6. 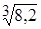 .
.
Литература обязательная
1. Арефьев К. П., Ивлев Е. Т., Тарбокова Т. В. Системы линейных уравнений: учебное пособие. – Томск: Изд. ТПУ, 1996.
2. Высшая математика. Часть I. Учебное пособие / К. П. Арефьев,
А. И. Нагорнова, Е. И. Подберезина, Г. П. Столярова, А. Н. Харлова. – Томск: Изд-во ТПУ, 2004. – 188 с.
3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в примерах и задачах. Часть I. – М.: Высшая школа, 1980.
4. Каплан И. А. Практические занятия по высшей математике. Часть I. – М., 1971.
Учебное издание
Date: 2015-09-02; view: 473; Нарушение авторских прав