Выпуклость и вогнутость кривой. Точки перегиба

Пусть кривая задана функцией .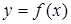

Определение 1. Кривая называется выпуклой вверх (вниз) на отрезке 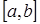, если все точки кривой находятся ниже (выше) любой касательной к графику функции.

Определение 2. Точка , отделяющая вогнутую часть от выпуклой, называется точкой перегиба графика функции .

Теорема. Если функция дважды дифференцируема на некотором промежутке, причем 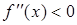для любого 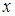из этого промежутка, то на этом промежутке график функции выпуклый, если , то график вогнутый.

Из теоремы следует, что для нахождения промежутков (выпуклости) вогнутости надо найти вторую производную функции и определить промежутки, где она положительна (отрицательна). Необходимым условием существования точки перегиба является обращение в нуль второй производной или ее отсутствие в точке , то есть условие или .
В случае выполнения одного из этих условий точка называется критической точкой второго рода.

Достаточным условием того, что точка - точка перегиба является смена знака второй производной при переходе через критические точки второго рода.

Правило нахождения интервалов выпуклости, вогнутости и точек перегиба функции.

1. Указать область определения функции.

2. Найти критические точки второго рода, принадлежащие области определения функции.

3. Определить знак второй производной в каждом интервале области определения между соседними критическими точками.

4. По знаку 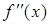установить интервалы выпуклости, вогнутости и по смене знака второй производной в окрестности точки – наличие или отсутствие точки перегиба.

Date: 2015-09-02; view: 425; Нарушение авторских прав