Наклонные и горизонтальные асимптоты

Определение. Прямая 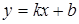называется наклонной асимптотой графика функции 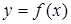при 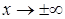,если эту функцию можно представить в виде , , 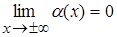т. е. разность между ординатами точек кривой и асимптоты при 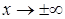есть бесконечно малая величина.

Теорема. Для того, чтобы график функции имел наклонную асимптоту, необходимо и достаточно, чтобы имели место соотношения:

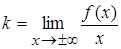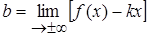, , причем эти пределы могут быть неравными 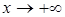при и при . Если , , 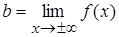получаем горизонтальную асимптоту 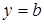. Таким образом, прямая 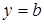является горизонтальной асимптотой кривой 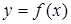, если .

Задача 2. Найти асимптоты графика функции .

Решение. . Вычислим =

= , .

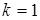Найдем : .

Получим уравнение асимптоты ; убедимся, что утверждение теоремы выполняется. Преобразуем функцию, выделив целую часть.

, где ,

Кроме того, функция имеет вертикальную асимптоту 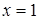, т. к.

, .

Задача 3. Найти асимптоты графика функции .

Решение. Найдем . При функция терпит разрыв второго порядка, т. к.

.

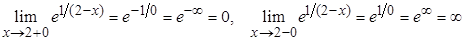Таким образом, является вертикальной асимптотой.

Найдем горизонтальные асимптоты.

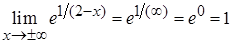, следовательно, 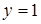является горизонтальной асимптотой.

Date: 2015-09-02; view: 441; Нарушение авторских прав