Производные и дифференциалы высших порядков

Определение 1. Производной второго порядка от функции называется производная от производной первого порядка и обозначается символом или , или .

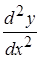Пример. , , .

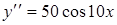Определение 2. Производной -го порядка называется производная первого порядка от производной 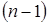-го порядка и обозначается 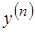или , или .

Пример. . Найти .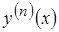

, , ! ,

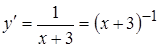! , используя метод математической индукции, запишем формулу производной -го порядка !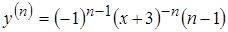

Определение 3. Дифференциалом высшего порядка функции называется дифференциал от дифференциала 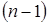-го порядка:

, в частности 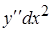, здесь .

Пример: 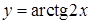. Найти .

, ;

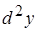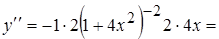
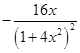Тогда .

Производная второго порядка от функции, заданной параметрически.

Если 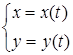, то производные , , 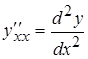последовательно могут быть вычислены по формулам:

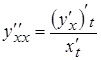= , , и т. д.

Для производной второго порядка имеет место формула .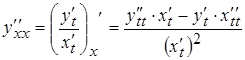

Пример. Найти от функции

Решение. Найдем сначала , ,

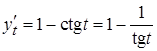тогда , .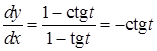

Правило Лопиталя. Раскрытие неопределенностей при вычислении пределов

Теорема. Предел отношения двух бесконечно малых или двух бесконечно больших существует и равен пределу отношения их производных:

, если выполняются условия:

1) функции и дифференцируемы в некоторой окрестности точк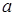и и в этой окрестности.

2)

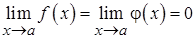
(или ).

3) существует конечный или бесконечный.

Здесь 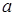может быть числом или одним из символов: .

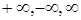Задача 1. Вычислить пределы: а) 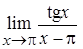, б) .

Решение. а) Подставив предельное значение аргумента 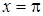, получаем неопределенность 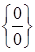, т.к. 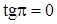, 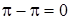и функции дифференцируемы.

Найдем .

б) При имеем неопределенность . Применим правило Лопиталя: 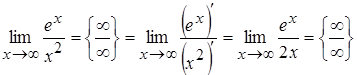. Полученный предел снова представляет неопределенность вида , применяя еще раз правило Лопиталя, найдем .

Другие виды неопределенностей , , 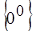можно свести к виду 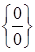или .

Задача 2. Найти предел .

Решение. Подставим предельное значение аргумента, получим неопределенность 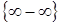, которая легко сводится к частному:

=

= .

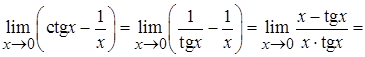
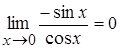Date: 2015-09-02; view: 490; Нарушение авторских прав