
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Производная неявной функции
|
|
Пусть уравнение  не разрешено относительно функции
не разрешено относительно функции  , т.е. функция
, т.е. функция  задана неявно. Чтобы найти производную
задана неявно. Чтобы найти производную 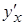 , надо продифференцировать левую и правую часть уравнения, учитывая, что
, надо продифференцировать левую и правую часть уравнения, учитывая, что 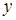 есть функция аргумента
есть функция аргумента 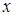 . Рассмотрим это правило на примерах.
. Рассмотрим это правило на примерах.
Пример 1. Найти 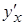 , если а)
, если а)  , б)
, б)  .
.
Решение: а) 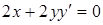 , выразив
, выразив  , получим
, получим 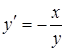 .
.  ;
;
б) дифференцируя обе части этого уравнения, получим уравнение относительно  :
: 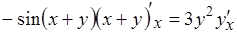 ,
, 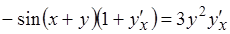 ;найдем теперь
;найдем теперь 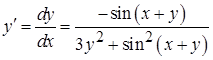 .
.
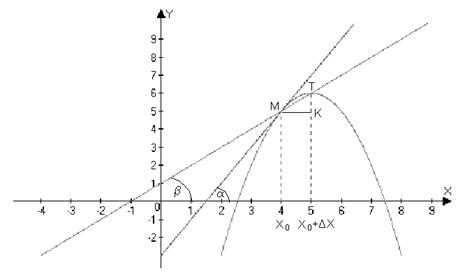 |
Геометрический смысл производной
Здесь 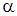 – угол наклона касательной к графику функции
– угол наклона касательной к графику функции 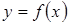 и точке
и точке 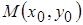 . Через две точки
. Через две точки 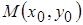 и
и  кривой
кривой 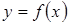 проведем секущую
проведем секущую  , ее угловой коэффициент
, ее угловой коэффициент 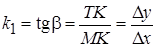 . Двигая точку
. Двигая точку  по кривой к точке
по кривой к точке  , мы будем поворачивать секущую вокруг точки
, мы будем поворачивать секущую вокруг точки  , в результате секущая стремится занять положение касательной, проведенной к графику в точке, а угол
, в результате секущая стремится занять положение касательной, проведенной к графику в точке, а угол  стремится к углу
стремится к углу 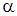 – наклона касательной, т.е.
– наклона касательной, т.е. 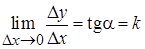 ,
,
где  – угловой коэффициент касательной. Известное уравнение прямой
– угловой коэффициент касательной. Известное уравнение прямой  используем как уравнение касательной, проведенной к графику функции
используем как уравнение касательной, проведенной к графику функции  в точке
в точке  , с угловым коэффициентом
, с угловым коэффициентом  . Тогда уравнение касательной примет вид
. Тогда уравнение касательной примет вид
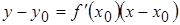 (3)
(3)
Задача. Найти уравнение касательной к графику функции
а) 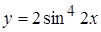 в точке
в точке  , б)
, б) 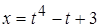 ,
,  в точке
в точке  .
.
Решение. а) Сначала вычислим ординату точки касания  . Затем производную в точке
. Затем производную в точке 
 ,
,
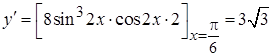 . Это угловой коэффициент касательной.
. Это угловой коэффициент касательной.
Подставим найденные параметры в уравнение (3)
 – искомая касательная;
– искомая касательная;
б) кривая задана параметрически; найдем координаты точки касания, подставив значение параметра в уравнение кривой: 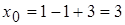 ,
, 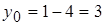 . Для отыскания углового коэффициента
. Для отыскания углового коэффициента  воспользуемся формулой
воспользуемся формулой 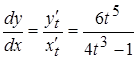 ,
,  , теперь запишем уравнение касательной
, теперь запишем уравнение касательной  , или
, или 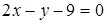 .
.
Date: 2015-09-02; view: 493; Нарушение авторских прав