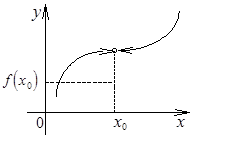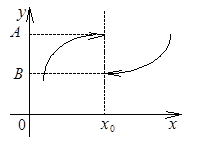Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Непрерывность функций
|
|
Определение 1. Функция 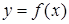 с областью определения
с областью определения  называется непрерывной в точке
называется непрерывной в точке 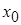 , если выполнены следующие условия:
, если выполнены следующие условия:
1) функция 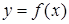 определена в точке
определена в точке 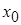 , т.е.
, т.е. 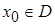 ;
;
2) существует  ;
;
3) 
Условие пункта 2 эквивалентно существованию равных односторонних пределов функции 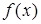 в точке
в точке 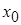 , т.е.
, т.е.

Если в точке 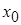 нарушено хотя бы одно из условий 1−3, то точка
нарушено хотя бы одно из условий 1−3, то точка 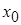 называется точкой разрыва функции
называется точкой разрыва функции 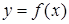 .
.
При исследовании функции на непрерывность пользуются следующей теоремой:
Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Определение 2. Если функция 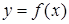 непрерывна в каждой точке некоторого интервала
непрерывна в каждой точке некоторого интервала  , где
, где  , то говорят, что функция непрерывна на этом интервале.
, то говорят, что функция непрерывна на этом интервале.
Следовательно, функция может иметь разрыв в точках, где она меняет способ своего задания или не определена.
Существуют следующие виды точек разрыва.
|
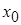 существует конечный
существует конечный
предел функции 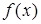 , но он не равен значению
, но он не равен значению
функции в этой точке, т.е.
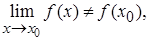
то такая точка называется точкой
разрыва I рода (устранимый разрыв).
2. Точка 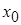 называется точкой разрыва I рода
называется точкой разрыва I рода
|
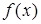 , если
, если
в этой точке существуют конечные
односторонние пределы функции
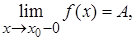
 ,
,
но они не равны между собой.
3.Точка 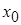 называется точкой разрыва II рода или точкой бесконечного разрыва, если хотя бы один из односторонних пределов функции
называется точкой разрыва II рода или точкой бесконечного разрыва, если хотя бы один из односторонних пределов функции 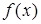 в точке
в точке 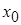 равен бесконечности
равен бесконечности 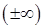 .
.

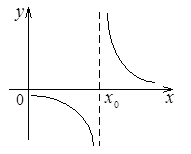
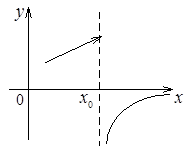
Пример. Исследовать функции на непрерывность, найти точки разрыва и определить их тип:
а) 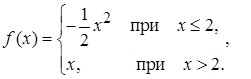
Данная функция определена на всей числовой оси. Она задана двумя различными формулами для интервалов  и
и 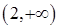 и может иметь разрыв в точке
и может иметь разрыв в точке  , где меняется способ ее задания. Найдем односторонние пределы в точке
, где меняется способ ее задания. Найдем односторонние пределы в точке  :
:
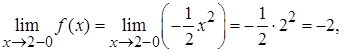
так как слева от точки  функция
функция 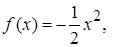
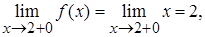
так как справа от точки  функция
функция  .
.
Таким образом, в точке  функция
функция 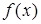 имеет конечные односторонние пределы, но они не равны между собой
имеет конечные односторонние пределы, но они не равны между собой 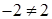 . Следовательно,
. Следовательно,  - точка разрыва I рода (точка скачка). Во всех остальных точках числовой оси данная функция непрерывна, так как формулы, которыми она задана определяют элементарные непрерывные функции. Построим график этой функции.
- точка разрыва I рода (точка скачка). Во всех остальных точках числовой оси данная функция непрерывна, так как формулы, которыми она задана определяют элементарные непрерывные функции. Построим график этой функции.

б) 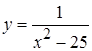
Функция  определена для всех значений кроме
определена для всех значений кроме  и
и 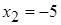 . Эта функция элементарная, значит, она непрерывна во всей области своего определения
. Эта функция элементарная, значит, она непрерывна во всей области своего определения 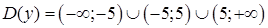 . В точках
. В точках  и
и 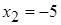 функция
функция 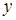 имеет разрывы, так как нарушается первое условие непрерывности. Чтобы определить характер разрыва в этих точках, найдем односторонние пределы
имеет разрывы, так как нарушается первое условие непрерывности. Чтобы определить характер разрыва в этих точках, найдем односторонние пределы
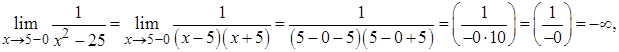

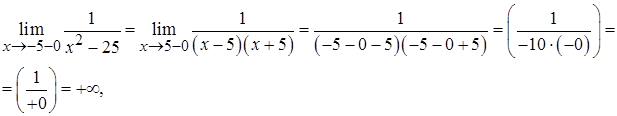
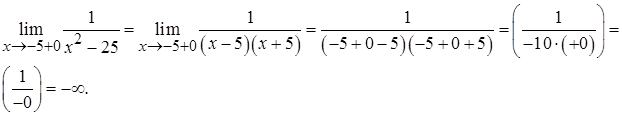 Поскольку все односторонние пределы равны бесконечности, функция
Поскольку все односторонние пределы равны бесконечности, функция 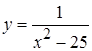 терпит в точках
терпит в точках  и
и 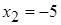 разрывы II рода. Построим график функции
разрывы II рода. Построим график функции
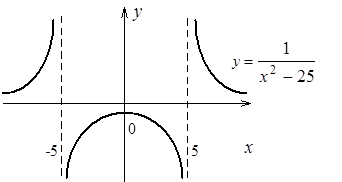
в) 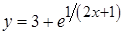 .
.
Функция определена и непрерывна на всей числовой оси, кроме точки  . Из этого следует, что в точке
. Из этого следует, что в точке  функция
функция 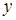 имеет разрыв. Найдем односторонние пределы
имеет разрыв. Найдем односторонние пределы


Так как предел справа в точке  равен бесконечности, заключаем, что
равен бесконечности, заключаем, что 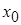 – точка разрыва II рода. Построим график функции
– точка разрыва II рода. Построим график функции 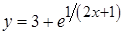
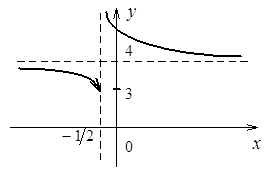
Варианты контрольных заданий для контрольной работы № 1
Date: 2015-09-02; view: 439; Нарушение авторских прав