
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Наближене обчислення визначених інтегралів
|
|
Задачі практики приводять іноді до інтегралів, точне обчислення яких за формулою Ньютона-Лейбніца неможливе або утруднене: первісна підінтегральної функції може не виражатися через елементарні функції, відшукання первісної може вимагати надто громіздких обчислень, нарешті підінтегральна функція може бути задана таблицею чи графіком, а не аналітичним виразом. В таких випадках інтеграл доводиться обчислювати наближено за допомогою чисельних методів. Ми розглянемо тут два такі методи, найпростіші і в той же час широко використовувані як при ручних обчисленнях, так і для програмування на ЕОМ.
|
 Нехай потрібно обчислити інтеграл
Нехай потрібно обчислити інтеграл 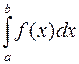 , де
, де  неперервна на відрізку
неперервна на відрізку 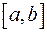 . Розіб’ємо відрізок
. Розіб’ємо відрізок 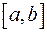 на
на 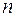 рівних частин точками
рівних частин точками 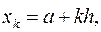
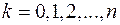 , де
, де  - крок розбиття (або крок інтегрування).
- крок розбиття (або крок інтегрування).
Позначимо 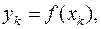
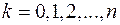 - ординати графіка підінтегральної функції в точках поділу. Задача полягає в тому, щоб дати вираз наближеного значення інтеграла
- ординати графіка підінтегральної функції в точках поділу. Задача полягає в тому, щоб дати вираз наближеного значення інтеграла 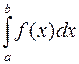 через ці ординати.
через ці ординати.
|
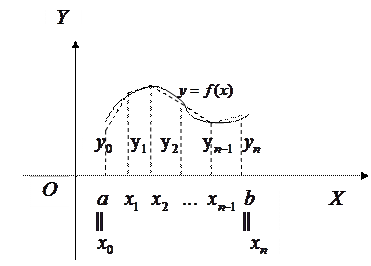
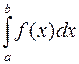 - площа фігури, обмеженої графіком підінтегральной функції, відрізком
- площа фігури, обмеженої графіком підінтегральной функції, відрізком 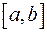 і крайніми ординатами
і крайніми ординатами 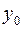 та
та 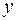 . Внаслідок виконаного розбиття відрізка
. Внаслідок виконаного розбиття відрізка 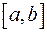 ця фігура розбита на
ця фігура розбита на 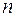 смужок шириною
смужок шириною 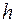 . Якщо
. Якщо 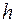 достатньо мале, то площу кожної такої смужки можна вважати наближено рівною площі трапеції з висотою
достатньо мале, то площу кожної такої смужки можна вважати наближено рівною площі трапеції з висотою 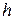 і основами, які дорівнюють ординатам, що обмежують смужку.
і основами, які дорівнюють ординатам, що обмежують смужку.
Тоді площа першої смужки 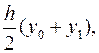
площа другої смужки 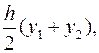
……
Площа 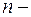 ої смужки
ої смужки  .
.
Додаючи ці площі, отримуємо наближене значення шуканого інтеграла:
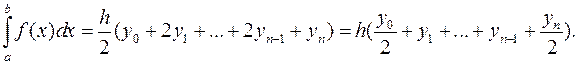
Це і є правило або формула трапецій. Можна довести, що гранична абсолютна похибка  цієї формули наближено пропорціональна
цієї формули наближено пропорціональна 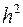 , тобто
, тобто  Таким чином, при зменшенні кроку
Таким чином, при зменшенні кроку 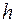 вдвічі похибка зменшується приблизно в 4 рази. Цим можна скористатися для наближеної (а для деяких функцій і точної) оцінки похибки. Для цього обирають число
вдвічі похибка зменшується приблизно в 4 рази. Цим можна скористатися для наближеної (а для деяких функцій і точної) оцінки похибки. Для цього обирають число 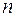 парним і обчислення інтеграла повторюють з подвоєним кроком. Нехай
парним і обчислення інтеграла повторюють з подвоєним кроком. Нехай 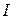 - точне значення інтеграла,
- точне значення інтеграла, 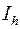 - результат обчислення з кроком
- результат обчислення з кроком 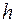 ,
, 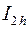 - результат обчислення з кроком
- результат обчислення з кроком 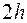 і
і  - похибка результата
- похибка результата 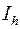 . Тоді
. Тоді 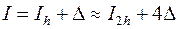 , звідки одержуємо оцінку
, звідки одержуємо оцінку  .
.
Приклад. Розглянемо застосування формули трапецій на прикладі інтеграла, точне значення якого відоме 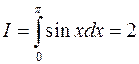 . Оберемо
. Оберемо 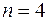 , тоді
, тоді 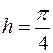 ,
, 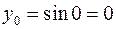 ,
, 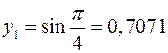 ,
, 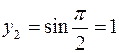 ,
,  ,
, 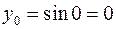 . Тоді
. Тоді  . Похибка близько
. Похибка близько 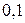 , тобто близько
, тобто близько  %.
%.
б) Правило Сімпсона (правило парабол).
За правилом Сімпсона число 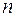 береться парним. Позначимо, як і раніше, через
береться парним. Позначимо, як і раніше, через 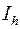 - результат обчислення інтеграла
- результат обчислення інтеграла 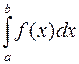 за правилом трапецій з кроком
за правилом трапецій з кроком 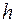 , а
, а 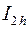 - теж саме з подвоєним кроком. Для похибки результату
- теж саме з подвоєним кроком. Для похибки результату 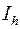 було одержано вираз
було одержано вираз 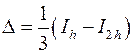 . Якщо до
. Якщо до 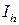 додати цю похибку, то результат очевидно стане точнішим. Тому природно покласти
додати цю похибку, то результат очевидно стане точнішим. Тому природно покласти
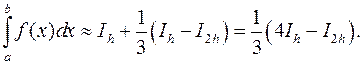
Замінимо  і
і 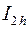 їх виразами:
їх виразами:
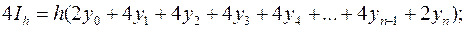
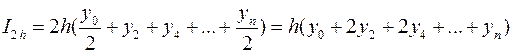 .
.
Тоді
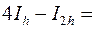
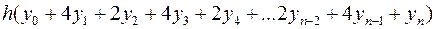 ,
,
звідки отримуємо
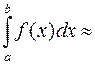
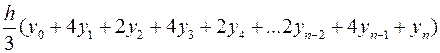 .
.
Це і є формула Сімпсона. Її називають також формулою парабол, тому що її можна отримати подібно до формули трапецій, але замінюючи на кожній парі частинних відрізків графік функції  параболою, яка проходить через ті ж точки (а не ламаною, як у методі трапецій). Правило Сімпсона при незначному збільшенні обсягу обчислень значно точніше, ніж правило трапецій. Його гранична похибка
параболою, яка проходить через ті ж точки (а не ламаною, як у методі трапецій). Правило Сімпсона при незначному збільшенні обсягу обчислень значно точніше, ніж правило трапецій. Його гранична похибка  наближено пропорціональна
наближено пропорціональна 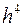 , тобто
, тобто 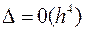 , і при зменшенні кроку в 2 рази зменшується в 16 разів.
, і при зменшенні кроку в 2 рази зменшується в 16 разів.
Приклад. Розглянемо знову  і оберемо, як і в попередньому прикладі,
і оберемо, як і в попередньому прикладі, 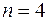 . Тоді
. Тоді 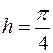 ,
, 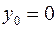 ,
, 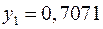 ,
,  ,
, 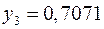 ,
, 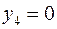 .
.
За формулою Сімпсона

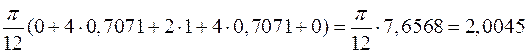 .
.
Похибка близько 0,0045, тобто близько 0,23% і порівняно з похибкою правила трапецій менша в 22 рази.
Date: 2015-09-02; view: 733; Нарушение авторских прав
