Действия с матрицами

Матрицы и действия с матрицами

Основные понятия.

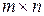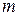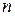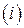Матрицей размера называется прямоугольная таблица чисел, содержащая строк и столбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойным индексом: , где первый индекс соответствует номеру строки, а второй индекс 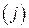– номеру столбца. Матрица размера 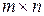может быть записана в одном из видов:

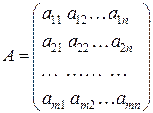
либо

При необходимости указать размер матрицы будем использовать

запись .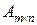

Элементы матрицы, имеющие одинаковые индексы, называются диагональными. Матрица, у которой ниже главной диагонали стоят нули, называется треугольной.

Матрица, состоящая из одной строки, называется матрицей-строкой, а матрица, состоящая из одного столбца – матрицей-столбцом. Обе такие матрицы называют также вектором.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается .

Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк (столбцов) порядком матрицы.

Квадратная матрица, у которой только диагональные элементы могут быть не равны нулю, называется диагональной матрицей.

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается .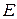

Перестановка в матрице строк со столбцами называется транспонированием матрицы. Матрица, полученная таким образом из матрицы , называется к ней транспонированной и обозначается :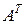

.

Заметим, что .

Действия с матрицами.

В математике матрица рассматривается как самостоятельный математический объект, с которым можно производить различные действия.

1. Сравнение матриц. Две матрицы равны, если они имеют одинаковый размер и соответствующие элементы равны:

.

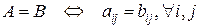2. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо умножить на это число все элементы матрицы:

.

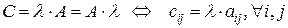3. Сложение (вычитание) матриц. Сложение (вычитание) матриц проводится поэлементно и возможно для матриц одного размера:

.

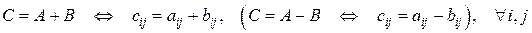Для перечисленных выше действий справедливы все алгебраические действия.

4. Умножение матриц. Матрицы перемножаются по правилу «строка на столбец»:

Рис.1

А именно, осуществляется операция, которая называется сумма произведений: элементы, соединенные одной линией перемножаются, а затем результаты умножения складываются. То есть, чтобы получить элемент 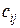матрицы 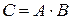надо каждый элемент 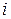−ой строки матрицы умножить на соответствующий по порядку элемент 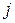−го столбца матрицы и результаты сложить. При записи знак умножения может быть опущен: .

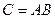Умножение матриц возможно только в случае, если число столбцов первой матрицы равно числу строк второй матрицы. Результат умножения – матрица, имеющая число строк, совпадающее с числом строк первой матрицы, и число столбцов равное числу столбцов второй матрицы. При умножении матрицы на вектор-столбец получаем вектор-столбец. При умножении матрицы на транспонированную к ней получаем квадратную матрицу.

Умножение матриц не коммутативно. Более того, при перестановке (коммутации) матриц подчас умножение не возможно. Те квадратные матрицы, для которых выполнено свойство , называются коммутативными.

Роль единицы при умножении матриц играет единичная матрица 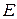. Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:

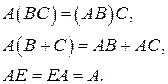
Отметим также свойство умножения и сложения для транспонированных матриц

.

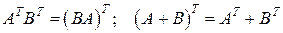6. Возведение в степень. Для квадратных матриц возможно возведение в натуральную степень, которое проводится как последовательное умножение. При этом очевидно, справедлив коммутативный закон умножения

.

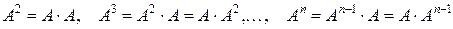►Пример 1.

а) Даны матрицы:

, , .

Выполнить указанные действия:

1) указать размер матрицы ,

2) записать элемент матрицы ,

3) найти: а) транспонированную матрицу 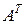, б) матрицу ,

4) вычислить ,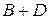

5) вычислить , ( 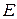- единичная матрица).

Решение.

1) Матрица имеет 3 строки и 4 столбца, следовательно, ее размер .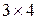

2) Элемент находится во второй строке и первом столбце матрицы : .

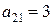3) Транспонированная матрица получается из исходной при замене строк на столбцы, а для записи матрицы 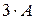необходимо все элементы матрицы умножить на три:

а) , б) .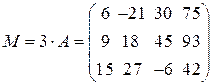

4) Матрицы и имеют одинаковый размер, следовательно, их можно складывать

.

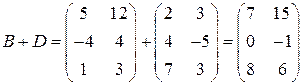5) Число столбцов матрицы равно числу строк матрицы . Следовательно, возможно умножение 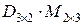, При этом получаем матрицу , имеющую три строки и три столбца:

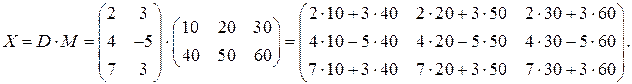
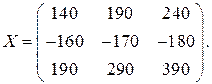
Аналогично возможно и умножение , получаем матрицу .

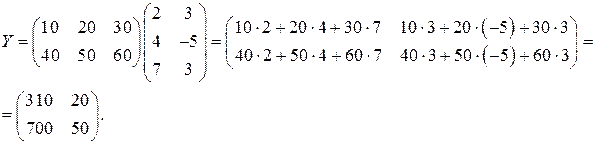
Так как складывать можно только матрицы одного размера, для нахождения матрицы 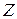необходимо взять единичную матрицу второго порядка:

. ◄

Date: 2015-09-02; view: 546; Нарушение авторских прав