Функции нескольких переменных

3.1. Примеры функций нескольких переменных

При изучении многих явлений приходится иметь дело с функциями двух и более переменных. Примеры:

S=xy. S – площадь прямоугольника, х и у – длины его сторон. S есть функция двух переменных.

V=xyz – объем прямоугольного параллелепипеда, длины ребер которого равны x, y, z. V – функция трех переменных.

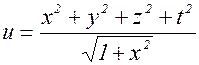– функция четырех переменных

x, y, z, t.

В дальнейшем мы будет рассматривать в основном функции двух переменных. Принципиальной разницы между функциями двух, трех и т.д. переменных нет, хотя технические трудности при вычислениях, безусловно, возрастают с ростом числа переменных.

3.2. Определение функции двух переменных. Область определения функции двух переменных

Определение 1. Если каждой паре (х, у) значений двух, независимых друг от друга переменных величин х и у из некоторой области их изменения D, соответствует определенное значение величины z, то z есть функция двух независимых переменных х и у, определенная в области D.

Обозначение: z = f (x, y), z = F (x, y) и т.д.

Определение 2. Совокупность пар (х, у) значений х и у, при которых определена функция z = f (x, y), называется областью определения или областью существования этой функции.

Примеры. Найти область определения функций:

1. z = 2x – y.

Выражение 2х – у имеет смысл при всех х и у. Следовательно, область определения D – вся плоскость хОу.

2.

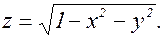
Область определения определяется неравенством 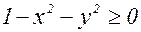или х² + у²£1. Очевидно, D – точки круга радиуса 1 с центром в начале координат. Граница круга входит в область определения.

3. z = ln(x + y).

Очевидно, х + у > 0, y >– x. Это полуплоскость над прямой у =– х (см. рис.).

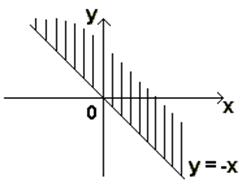
Точки прямой у=–х в область D не входят.

3.3. Геометрическое изображение функции двух переменных

Рассмотрим функцию

z = f(x, y), (3.3.1)

определенную в области G на плоскости хОу, и систему координат Оxyz. В каждой точке (х, у) области G проведем перпендикуляр к плоскости хОу и на нем отложим отрезок, равный f(x, y). Тогда в пространстве получим точку P(x,y,f(x,y)).

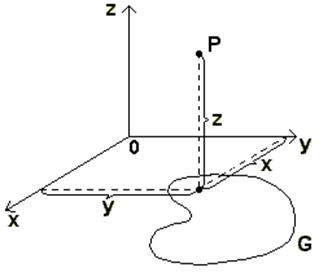
Геометрическое место таких точек, удовлетворяющих уравнению (3.3.1), называется графиком функции двух переменных. Уравнение (3.3.1) определяет в пространстве некоторую поверхность, которая и является графиком функции двух переменных.

Замечание. Функцию трех и более переменных графически изобразить невозможно.

3.4. Предел и непрерывность функции двух переменных

Введем важное понятие: окрестностью радиуса r точки М₀(х₀,у₀) называется совокупность всех точек (х,у), удовлетворяющих неравенству

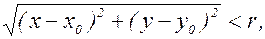
т.е. совокупность всех точек, лежащих внутри круга радиуса r с центром в точке М₀(х₀,у₀).

Рассмотрим функцию z=f(x,y), определенную в некоторой области G плоскости хОу. Рассмотрим точку М₀(х₀,у₀), лежащую внутри или на границе области G.

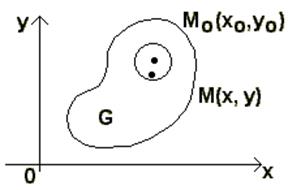
Определение 1. Число А называется пределом функции f(x,y) при стремлении точки М(х,у) к точке М₀(х₀,у₀), если для любого числа e>0 найдется такое число r > 0, что для всех точек М(х,у), для которых 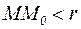, имеет место неравенство

.

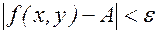При этом под 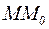понимается .

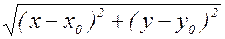Записывают так:

.

Определение 2. Пусть точка М₀(х₀,у₀) принадлежит области определения функции f(x,y). Функция z=f(x,y) называется непрерывной в точке (х₀,у₀), если имеет место равенство

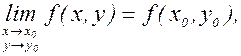
причем точка М(х,у) стремится к точке М₀(х₀,у₀) произвольным образом, оставаясь в области определения функции.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.

Примеры.

1. Функция z=x²+y² непрерывна в любой точке плоскости хОу. В самом деле, для любых х, у и произвольных Dх и Dу 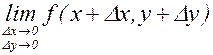равен:

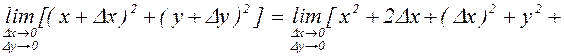
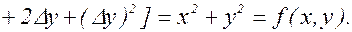
2. Покажем, что в точке х = 0, у = 0 эта функция не является непрерывной. Рассмотрим значения этой функции вдоль прямой у=kx (k = const), проходящей через начало координат

Отсюда ясно, что вдоль любого направления, определяемого значением k, функция сохраняет постоянное значение, определяемое величиной k. Но это и означает, что при подходе к началу координат по разным путям мы будем получать различные значения, т.е. функция предела не имеет.

3.5. Частные приращения и частные производные

Рассмотрим поверхность z=f (x, y), являющуюся графиком функции двух переменных (см. рис.).

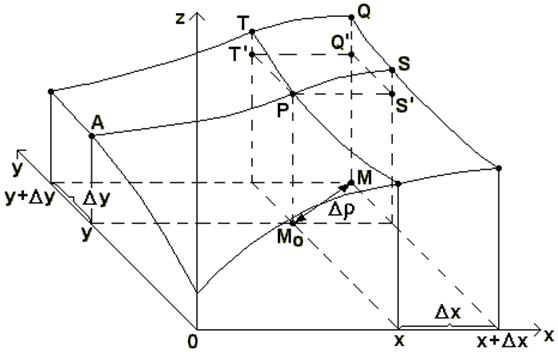
Изобразим линию пересечения этой поверхности с плоскостью у = const, параллельной плоскости хОz. Это линия АРS. В этой плоскости у сохраняет постоянное значение, поэтому при изменении х от х до х+Dх функция z получает приращение, которое называют частным приращением z по х:

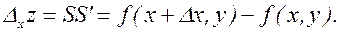(3.5.1)

Аналогично, если х сохраняет постоянное значение, а у получает приращение Dу, то z получает частное приращение по у D_уz:

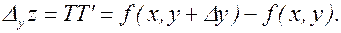(3.5.2)

Наконец, если задать приращение Dх аргументу х и приращение Dу аргументу у, получим приращение Dz, которое называется полным приращением функции z:

Dz = f(x+Dх, у+Dу) – f(х, у). (3.5.3)

На рисунке это QQ '.

Пример.

z = xy;

D_хz = (x + Dх) у – ху = уDх;

D_уz = х (у + Dу) – ху = хDу;

Dz = (х + Dх)(у + Dу) – ху = уDх + хD + DхDу.

Аналогичным образом определяются частные и полные приращения функции для любого числа переменных.

Определение. Частной производной по х от функции z=f(x,y) называется предел отношения частного приращения D_хz по х к приращению Dх при стремлении Dх к нулю:

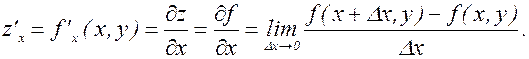
Аналогично

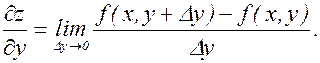
Пример.

z = x²sin y;

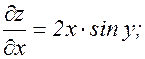
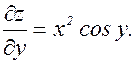
Из приведенного примера ясно, что при вычислении частной производной по х величина у считается постоянной, ее можно, например, выносить за знак производной, а при дифференцировании у по х результат равен нулю. Эти же замечания относятся и к случаю, когда вычисляется 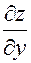; при этом х считается константой.

3.6. Полное приращение и полный дифференциал. Использование дифференциала для приближенных вычислений

Мы уже знаем, что полное приращение функции двух переменных z=f(x,y) записывается в виде:

Dz = f(х+Dх, у+Dу) – f(x,y).

Пусть в точке (х,у) существуют и непрерывны обе частные производные 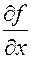и 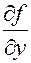. Перепишем Dz в виде

Dz = [f(x+Dx, y+Dy) – f(x, y+Dy)] + [f(x, y+Dy) – f(x,y)].

Применим теорему Лагранжа:

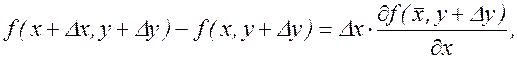
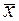Î(х, х+Dх);

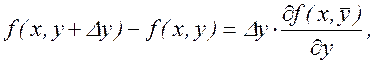
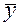Î(у, у+Dу);

Заметим, что в силу непрерывности частных производных

Но это означает, что

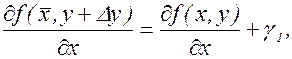
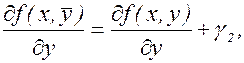
где g₁®0 и g₂®0, если Dх®0 и Dу®0 (или если ).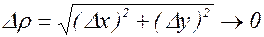

Тогда полное приращение Dz можно записать в виде

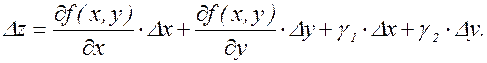(3.6.1)

Первые два члена в этой формуле – основные, а слагаемые g₁×Dх и g₂×Dу – бесконечные малые более высокого порядка, чем первые два члена.

Другими словами, можно дать следующее определение.

Определение. Функция z = f(x, y), полное приращение которой в данной точке (х,у) может быть представлено в виде (3.6.1), называется дифференцируемой в данной точке; линейная часть приращения называется полным дифференциалом:

dz=f '_x(x,y)Dx+f '_y(x,y)Dy.

Обычно обозначают Dх = dx, Dу = dy, а формула для полного дифференциала имеет вид

(3.6.2)

С точностью до бесконечно малых высшего порядка относительно Dr можно записать приближенное равенство:

Dz» dz, (3.6.3)

которое используется для приближенных вычислений.

Примеры.

1. z=xy. Найти полный дифференциал и полное приращение в точке (2;3) при Dх=0,1, Dу=0,2.

Dz = (х + Dх)(у + Dу) – ху = уDх + хDу + DхDу;

Dz=0,72; dz=0,7.

2. Задача. Вычислить объем материала, нужно для изготовления цилиндрического стакана следующих размеров:

- радиус внутреннего цилиндра R;

- высота внутреннего цилиндра H;

- толщина стенок и дна стакана l.

Точное решение:

V=p(R+l)²(H+l)–pR²H=p(2RHl+R²l+Hl²+2Rl²+l³). (*)

Приближенное решение:

f = pR²H – объем внутреннего цилиндра. Это функция двух переменных R и Н. Если увеличить R и Н на l, то функция f получит приращение Df. Тогда V=Df.

Приближенно:

, ,

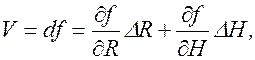
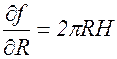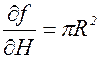V» p(2RHl + R²l). (**)

Сравнивая (*) и (**), замечаем, что эти выражения отличаются на величину p(Hl²+2Rl²+l³), состоящую из членов второго и третьего порядка малости относительно l (естественно, мы должны считать l<<R, l<<H).

Числовой пример: R=4 см, Н=20 см, l=0,1 см.

V=17,881 p –точное значение,

V»17,6 p – приближенное значение.

Ошибка .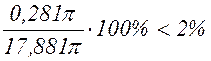

3.7. Сложная функция и ее полная производная

Пусть

z=F(u,v), (3.7.1)

а u и v являются функциями независимых переменных х и у.

u=j(x,y), v=y(x,y). (3.7.2)

В этом случае z есть сложная функция х и у. Будем рассматривать вопрос о частных производных и 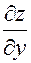. Дадим приращение Dх, не меняя у. Тогда u и v получат приращения D_хu и D_хv:

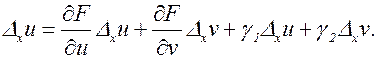
Здесь g₁ и g₂ – бесконечно малые при Dх®0. Разделим последнее равенство на Dх и перейдем к пределу при Dх®0:

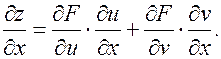(3.7.3)

Аналогично

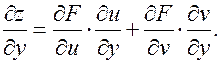(3.7.4)

(3.7.3) и (3.7.4) – формулы для частных производных сложной функции.

Пример.

z=ln(u²+v), 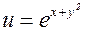; v=x²+y. Найти и .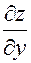

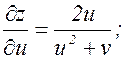
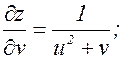
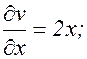
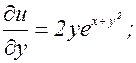
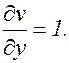
Тогда

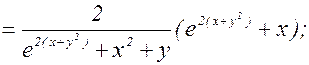
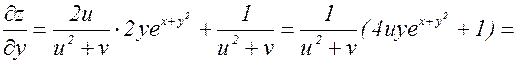
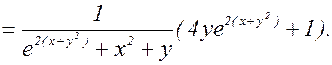
Для случая большего числа переменных формулы (3.7.3) и (3.7.4) естественным образом обобщаются.

Рассмотрим следующий случай: дана функция z=F(x,y,u,v), где y,u,v зависят только от одной переменной х:

y=f(x), u=j(x), v=y(x).

В этом случае, по сути дела, z является функцией только одной переменной х и можно ставить вопрос о нахождении производной (в отличие от эта производная называется полной производной).

Очевидно

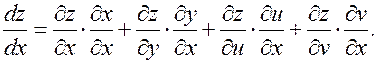
Но 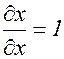, а производные 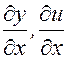и 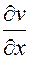являются по существу не частными, а полными производными, т.к. у, u и v зависят только от х:

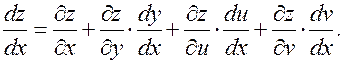(3.7.5)

Эта формула носит название формулы полной производной (в отличие от частной производной ).

Пример.

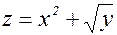; у=sin x. Найти .

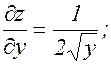
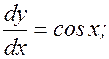
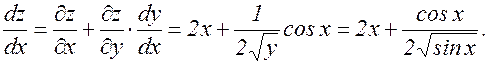
3.8. Производная неявно заданной функции

Если неявная функция одной переменной задана уравнением

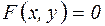, (3.8.1)

то производная 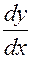находится по известной формуле:

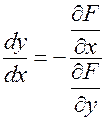. (3.8.2)

Формула (3.8.2) носит название производной неявно заданной функции одной переменной.

По аналогии неявная функция двух переменных (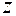 есть функция 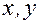) задается уравнением

.

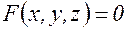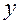Если теперь искать, например частную производную , то переменная считается постоянной и можно действовать по формуле (3.8.2). Тогда

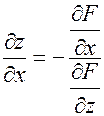. (3.8.3)

Аналогично

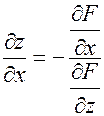. (3.8.4)

Разумеется, в формулах (3.8.3) и (3.8.4) следует считать 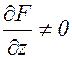. Эти формулы обобщаются на любое число переменных.

Пример.

Неявная функция трех переменных задана соотношением

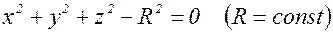. Найти и .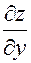

Пусть 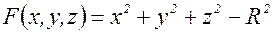. Тогда

.

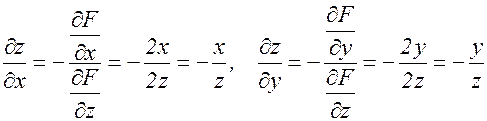3.9. Частные производные высших порядков

Пусть дана функция двух переменных z=f(x,y). Ее частные производные 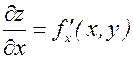и , вообще говоря, являются функциями двух переменных х и у. Поэтому эти функции можно снова дифференцировать по х и у. Таких частных производных второго порядка всего четыре, т.к. каждую из производных и 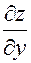можно дифференцировать как по х, так и по у.

Эти производные обозначаются так:

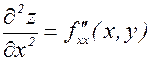– дифференцируем два раза подряд по х;

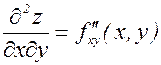– сначала дифференцируем по х, затем по у;

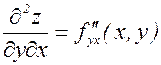– сначала дифференцируем по у, затем по х;

– два раза дифференцируем по у.

Можно продолжать этот процесс, дифференцируя вторые производные по х или у и получая третьи производные и т.д.

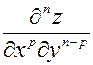– частная производная n -го порядка, дифференцирование ведется сначала р раз по х, затем n–p раз по у.

Аналогично определяются производные любого порядка от функции любого числа переменных.

Пример. Вычислить производные 2-го порядка функции f(x,y)=х²у+у³.

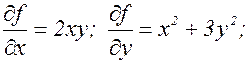
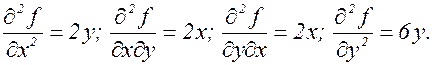
В данном примере оказалось, что 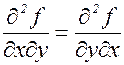, т.е. смешанная производная по х и у оказалась не зависящей от порядка дифференцирования. Оказывается, что это совсем не случайно.

Теорема (без доказательства).

Если функция f(x,y) и ее частные производные до второго порядка включительно определены и непрерывны в окрестности точки (х,у), то в этой окрестности

.

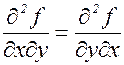
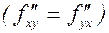Из этой теоремы следует, что смешанные частные производные второго порядка не зависят от порядка дифференцирования. Это свойство дифференцируемых функций следует иметь в виду при выполнении практических расчетов.

Date: 2015-09-02; view: 1057; Нарушение авторских прав