Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Примеры с решениями. П р и м е р 1. Найти производную функции
|
|
П р и м е р 1. Найти производную функции
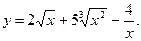
Р е ш е н и е. Используя основные правила дифференцирования и формулу (2), находим:
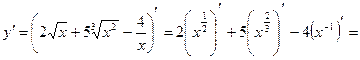
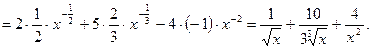
О т в е т: 
П р и м е р 2. Найти производную функции
Р е ш е н и е. Применив формулу для производной частного
,
получаем:
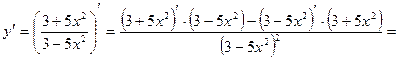
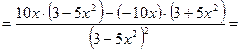
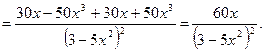
О т в е т: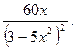 
П р и м е р 3. Дана функция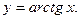 
Найти вторую производную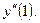 
Р е ш е н и е. Последовательно вычисляем:
= 
,
,
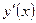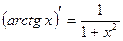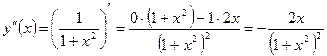О т в е т: 
.
П р и м е р 4. Найти производную функции
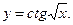
Р е ш е н и е. Данная функция является сложной:
, где 
Отсюда находим:
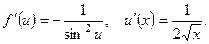
Поэтому, воспользовавшись правилом дифференцирования сложной функции, получаем:
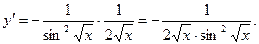
О т в е т: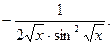 
П р и м е р 5. Написать уравнения касательной и нормали к графику функции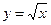 
в точке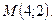 
Р е ш е н и е. Найдем производную функции 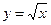в точке 
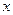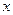( >0):
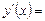
Найдем числа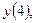 
:
, 
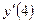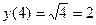Поэтому уравнение касательной в точке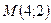 
имеет вид:
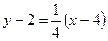, то есть 
.
О т в е т: .
П р и м е р 6. Вычислить предел
.
Р е ш е н и е. Воспользуемся правилом Лопиталя:
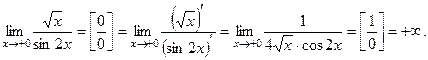
О т в е т: +¥.
П р и м е р 7. Вычислить предел
.
Р е ш е н и е. Воспользуемся правилом Лопиталя:
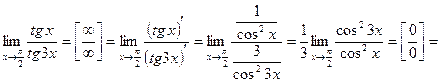
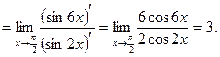
О т в е т: 3.
П р и м е р 8. Вычислить предел
.
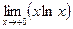Р е ш е н и е. Раскроем неопределенность:
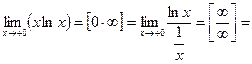
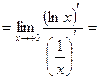
О т в е т: 0.
П р и м е р 9. Вычислить предел
.
Р е ш е н и е. Раскроем неопределенность:
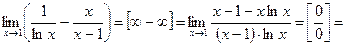
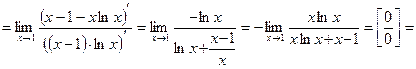
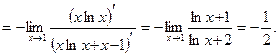
О т в е т: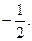 
П р и м е р 10. Вычислить предел
.
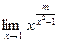Р е ш е н и е. Раскроем неопределенность:
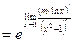
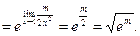
О т в е т: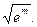 
П р и м е р 11. Найти дифференциал функции
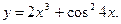
Р е ш е н и е. Найдем производную функции:
.
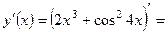
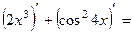
Следовательно, по определению дифференциала получаем:
.
О т в е т: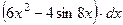 
.
Date: 2015-09-02; view: 407; Нарушение авторских прав