
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры с решениями. П р и м е р 1. Исследовать функцию на Непрерывность
|
|
П р и м е р 1. Исследовать функцию 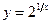 на непрерывность. Определить тип ее точек разрыва.
на непрерывность. Определить тип ее точек разрыва.
Р е ш е н и е. Функция 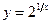 является элементарной. Область определения функции:
является элементарной. Область определения функции: 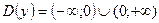 . Следовательно, по теореме 5 функция
. Следовательно, по теореме 5 функция 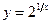 непрерывна во всех точках
непрерывна во всех точках 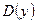 .
.
Исследуем на непрерывность точку 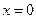 . Она − предельная точка множества
. Она − предельная точка множества 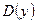 , но не принадлежит
, но не принадлежит 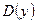 . Следовательно, точка
. Следовательно, точка 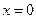 − точка разрыва функции
− точка разрыва функции 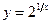 .
.
Определим тип точки разрыва 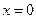 , для чего вычислим в этой точке односторонние пределы. Получаем:
, для чего вычислим в этой точке односторонние пределы. Получаем:
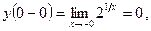
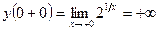
 (см. рис. 1).
(см. рис. 1).
 у y=
у y= 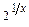
 |
 1
1
 O x Рис. 1
O x Рис. 1
О т в е т: непрерывна в области 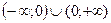 ,
,
точка 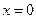 является точкой разрыва второго рода.
является точкой разрыва второго рода.
П р и м е р 2. Исследовать функцию

на непрерывность. Определить тип ее точек разрыва.
Р е ш е н и е. Функции 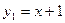 и
и 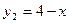 являются элементарными, определены на всей вещественной прямой. Следовательно, по теореме 5 они непрерывны во всех точках
являются элементарными, определены на всей вещественной прямой. Следовательно, по теореме 5 они непрерывны во всех точках  . Значит, в частности, функция
. Значит, в частности, функция 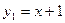 непрерывна на отрезке
непрерывна на отрезке 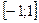 , функция
, функция 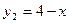 непрерывна на промежутке
непрерывна на промежутке 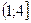 .
.
Следовательно, функция

непрерывна во всех точках промежутков  и
и 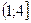 , а также непрерывна слева в точке
, а также непрерывна слева в точке  .
.
Таким образом, остается исследовать точку  на непрерывность. Вычисляем:
на непрерывность. Вычисляем:
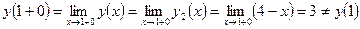 ,
,
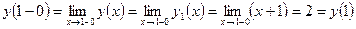
(см. рис. 2).
 у
у


 3
3

 2
2
 -1 O 1 4 x
-1 O 1 4 x
Рис. 2
О т в е т: непрерывна на промежутках  и
и 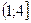 ,
,
непрерывна слева в точке  ,
,
точка  – точка разрыва первого рода.
– точка разрыва первого рода.
П р и м е р 3. Найти асимптоты кривой
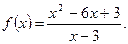
Р е ш е н и е. 1) Функция 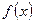 является элементарной. Она не определена в точке
является элементарной. Она не определена в точке 
Вычислим в этой точке односторонние пределы:

Таким образом, 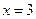 − точка разрыва второго рода функции
− точка разрыва второго рода функции 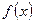 , а значит,
, а значит, 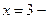 уравнение вертикальной асимптоты графика этой функции.
уравнение вертикальной асимптоты графика этой функции.
2) Найдем наклонные асимптоты:
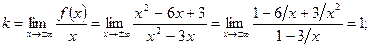
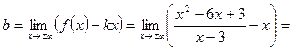
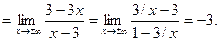
Следовательно, прямая 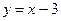 является для графика функции
является для графика функции 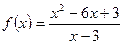 наклонной асимптотой при
наклонной асимптотой при 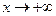 и при
и при 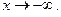
О т в е т: 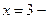 вертикальная асимптота;
вертикальная асимптота;
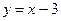 - наклонная асимптота
- наклонная асимптота
при 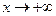 и
и 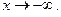
П р и м е р 4. Найти интервалы возрастания, убывания и экстремумы функции
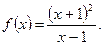
Р е ш е н и е. 1)  .
.
2) Найдем производную 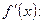
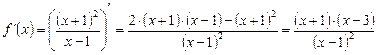 .
.
Значит, функция 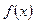 дифференцируема и
дифференцируема и 
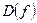 .
.
3) Найдем критические точки функции 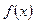 :
:
 при
при 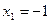 и
и  ;
;
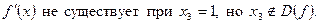
4) Разобьем область  на интервалы найденными критическими точками. По контрольным точкам определим знак производной
на интервалы найденными критическими точками. По контрольным точкам определим знак производной 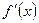 в этих интервалах и составим таблицу:
в этих интервалах и составим таблицу:
 |
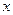
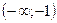
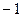
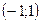 1
1 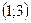 3
3 
 |
знак 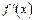 + 0 - - 0 +
+ 0 - - 0 +






вывод о  max min
max min
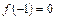

 |
О т в е т: интервалы возрастания: 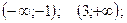
интервалы убывания: 
точка  точка максимума,
точка максимума, 
точка 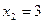 – точка минимума,
– точка минимума, 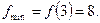
П р и м е р 5. Найти точки перегиба, интервалы выпуклости и вогнутости кривой 
Р е ш е н и е. 1) 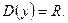
2) Найдем вторую производную 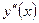 :
:
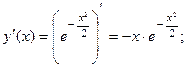
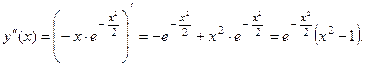
Отсюда, в частности, заключаем: 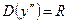 .
.
3) Найдем нули функции 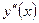 :
:
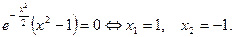
4) Разобьем область 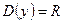 на интервалы точками -1 и 1. По контрольным точкам определим знак
на интервалы точками -1 и 1. По контрольным точкам определим знак 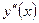 на этих интервалах и составим таблицу:
на этих интервалах и составим таблицу:
 |

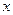
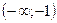 -1
-1 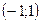 1
1 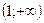
знак 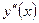 + 0 - 0 +
+ 0 - 0 +

вывод о вогнутый точка выпукл. точка вогнутый

 графике функции перегиба перегиба
графике функции перегиба перегиба

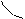

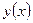
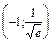
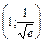
О т в е т: интервал выпуклости: 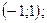
интервалы вогнутости: 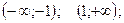
точки перегиба: 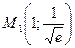 и
и 
П р и м е р 6. Исследовать функцию
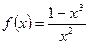
и построить ее график.
Р е ш е н и е. Выполним исследование свойств функции по описанной выше схеме.
1) 
2) Функция не является периодической, так как не существует числа Т> 0, для которого 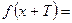
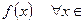

3) Исследуем функцию на четность или нечетность:

Следовательно,  и
и 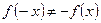 . Значит,
. Значит, 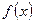 − функция общего вида.
− функция общего вида.
4) Найдем точки пересечения графика с осями координат:
а) с Ох: 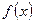 =0 при
=0 при 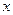 =1. Следовательно, график функции
=1. Следовательно, график функции 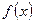 пересекает ось Ох в точке (1;0);
пересекает ось Ох в точке (1;0);
б) с Оу: график функции 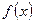 не пересекает ось Оу, так как 0
не пересекает ось Оу, так как 0 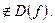
4) Найдем интервалы знакопостоянства функции:
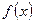 >0 на
>0 на 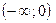 и
и 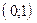 ,
, 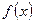 <0 на
<0 на 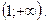
6) Исследуем функцию 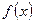 на непрерывность. Она − элементарная, а значит, непрерывна во всех точках области определения. В точке х =0 функция не определена, но эта точка является предельной для области определения.
на непрерывность. Она − элементарная, а значит, непрерывна во всех точках области определения. В точке х =0 функция не определена, но эта точка является предельной для области определения.
Значит, точка х =0 – точка разрыва функции.
Определим тип точки разрыва, вычислив в ней односторонние пределы 

Значит точка х =0 - точка разрыва второго рода функции 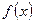 .
.
7) Найдем асимптоты графика.
В точке х =0 функция имеет разрыв второго рода, следовательно, прямая х =0 − вертикальная асимптота графика функции 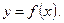
Найдем наклонные асимптоты графика:
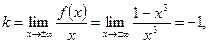

Следовательно, прямая 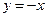 является наклонной асимптотой кривой при
является наклонной асимптотой кривой при 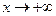 и при
и при 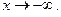
8) Найдем интервалы возрастания, убывания функции, ее экстремумы.
а) Найдем производную 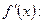
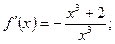

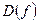 .
.
б) Найдем критические точки:

функция 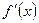 не существует в точке
не существует в точке 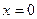 , но
, но 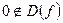 .
.
в) Составим таблицу:
 |
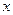

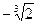
 0
0 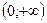
 |
 знак
знак



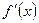 0
0
 |

 вывод
вывод 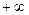


о 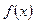
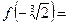

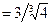

Следовательно, интервал возрастания:  ;
;
интервалы убывания:  и
и 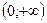 ;
;
точка 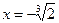 есть точка минимума,
есть точка минимума,
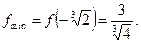
9) Найдем интервалы выпуклости, вогнутости, точки перегиба графика функции.
а) Найдем вторую производную 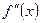 :
:
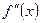 =
= 
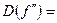
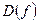 .
.
б) Найдем точки, в которых 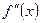 =0 или
=0 или 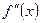 не существует:
не существует:
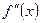 ¹0
¹0 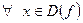 ;
;
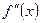 не существует при х =0, но 0
не существует при х =0, но 0 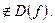
Следовательно, кривая не имеет точек перегиба.
в) Составим таблицу:
 |



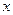
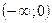 0
0 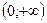

 знак
знак  + +
+ +


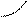
 вывод о вогнутый вогнутый
вывод о вогнутый вогнутый
графике

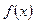
Следовательно, график функции не имеет точек перегиба и всюду вогнутый.
Для построения графика функции полученные результаты исследования удобно свести в таблицу:
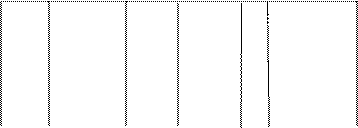 |



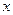

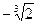
 0
0 


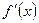 - 0 + -
- 0 + -





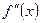 + + + +
+ + + +


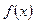
 min
min 


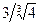

Итогом проведенных исследований является график функции
 (см. рис.3).
(см. рис.3).

 у
у




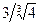

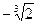 О 1 х
О 1 х
Рис. 3
П р и м е р 7. Исследовать функцию

и построить ее график.
Р е ш е н и е. Функция является элементарной.
1) 
2) Функция не является периодической, так как не существует числа Т >0, для которого 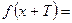
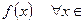

3) Так как область определения функции не является симметричной относительно начала координат, то изучаемая функция не может быть четной или нечетной, то есть функция  общего вида.
общего вида.
4) Находим точки пересечения графика функции с осями координат:
а) с Ох: 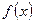 =0
=0 
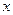 =1.
=1.
Следовательно, график функции 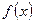 пересекает ось Ох в точке (1;0).
пересекает ось Ох в точке (1;0).
б) с Оу: график функции 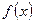 не пересекает ось Оу, так как 0
не пересекает ось Оу, так как 0 
5) Найдем промежутки знакопостоянства функции:
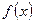 >0
>0 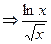 >0
>0 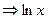 >0
>0 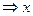 >1.
>1.
Следовательно, с учетом области определения функция положительна на интервале 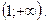 Аналогично,
Аналогично, 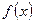 <0 на интервале
<0 на интервале 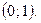
6) Функция непрерывна во всех точках области определения. В точке х =0 функция не определена, но эта точка является предельной для множества  Следовательно, точка х =0 – точка разрыва функции
Следовательно, точка х =0 – точка разрыва функции 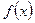 .
.
Вычислим 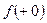 :
:
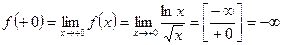 .
.
Значит, точка х =0 - точка разрыва второго рода.
7) В точке х =0 функция имеет разрыв второго рода, следовательно, прямая х =0 является вертикальной асимптотой графика функции 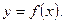
Найдем наклонную асимптоту 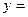 kx+b графика функции
kx+b графика функции 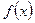 при
при 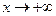 . Используя правило Лопиталя, находим:
. Используя правило Лопиталя, находим:
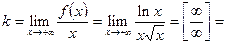
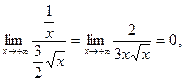
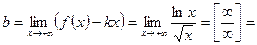
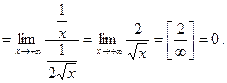
Следовательно, прямая  - наклонная асимптота кривой при
- наклонная асимптота кривой при 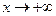 .
.
При 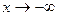 наклонная асимптота не существует, так как функция не определена на промежутке
наклонная асимптота не существует, так как функция не определена на промежутке  .
.
8) Исследуем функцию на возрастание, убывание и найдем ее экстремумы.
а) Найдем производную 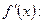
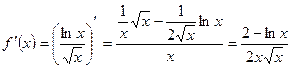 ,
, 
 .
.
б) Найдем критические точки:

функция  не существует в точке
не существует в точке  , но
, но 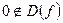 .
.
в) Составим таблицу:
 |
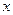
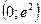


 |
знак

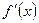 + 0
+ 0
 |
вывод max
о 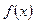

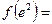
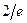 0
0
 |
Следовательно, интервал возрастания: 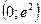 ;
;
интервал убывания:  ;
;
точка 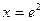 является точкой максимума,
является точкой максимума, 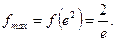
9) Исследуем график функции на выпуклость, вогнутость, наличие точек перегиба.
а) Найдем вторую производную 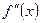 :
:
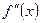 =
= 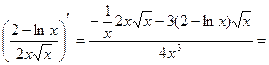
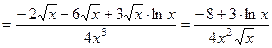 ,
, 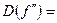
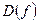 .
.
б) Найдем точки, в которых 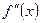 =0 или
=0 или 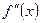 не существует:
не существует:
 ;
;
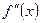 не существует при
не существует при 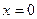 , но 0
, но 0 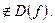
Следовательно, кривая имеет точку перегиба 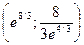 .
.
в) Составим таблицу:
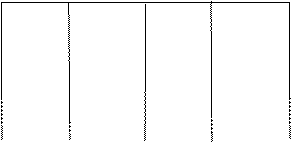 |

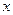
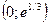


 знак
знак


 0
0
 |

 вывод о выпуклый точка вогнутый
вывод о выпуклый точка вогнутый
 графике перегиба
графике перегиба

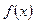
Следовательно, график функции выпуклый в интервале 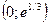 ; вогнутый в интервале
; вогнутый в интервале  ,
, 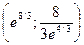 – точка перегиба.
– точка перегиба.
Для построения графика функции удобно свести в единую таблицу полученные выше результаты исследований:
 |

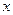


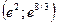


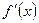 + 0 ― ― ―
+ 0 ― ― ―
 |

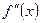 ― ― ― 0 +
― ― ― 0 +
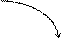


 mах точка
mах точка
2/е перегиба


 0
0
Итогом проведенного исследования является график функции
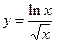 (см. рис. 4).
(см. рис. 4).
 у
у








О 1 
 х
х
Рис. 4
Date: 2015-09-02; view: 3962; Нарушение авторских прав