Уравнения в полных дифференциалах

Уравнение

(5.1)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции u (x, y):

.

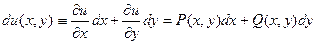Для того чтобы уравнение (5.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы

.

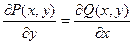(5.2)

Если известна функция, полным дифференциалом которой является левая часть уравнения (5.1), то все решения этого уравнения удовлетворяют условию u (x, y)= C, где С - произвольная постоянная.

Чтобы найти функцию u (x, y), воспользуемся равенствами:

.

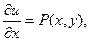(5.3)

Интегрируя первое из этих равенств по x, считаем y постоянным, и поэтому константа интегрирования может зависеть от у:

,

(5.4)

где 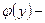произвольная дифференцируемая функция, F (x, y)- первообразная от P (x, y). Подберем функцию 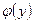так, чтобы удовлетворялось второе из соотношений (5.3). Для этого продифференцируем (5.4) по у и результат приравняем к 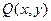. Таким образом, получим уравнение для определения функции :

.

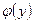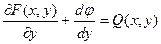(5.5)

Из (5.5) определяем 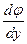и, интегрируя, находим 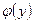. Подставляя эту найденную функцию в соотношение (5.4), получаем искомую функцию u (x, y).

Пример 1. Решить уравнение (2 xy +3 y ²) dx + (x²+6 xy -3 y ²) dy = 0.

D В данном случае , .

, .

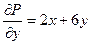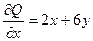Следовательно, , и левая часть данного уравнения является полным дифференциалом некоторой функции 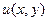. Имеем

, .

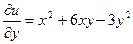Из первого уравнения находим

.

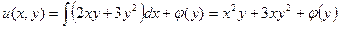Для определения функции 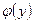дифференцируем полученное равенство по у и приравниваем выражению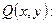

,

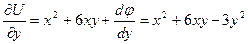т.е. 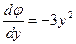. Отсюда . Поэтому 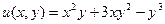. Общее решение записывается в виде

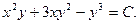Ñ

Пример 2. Решить уравнение .

D Это уравнение в полных дифференциалах, т.к.

.

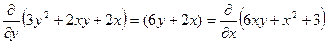Функцию u (x, y) найдем из уравнений . Интегрируя второе из этих уравнений по у, считая х постоянным, имеем: где − произвольная дифференцируемая функция. 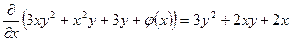. Следовательно,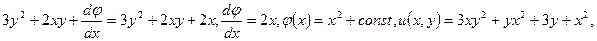

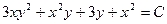. Ñ

Пусть левая часть уравнения (5.1) не есть полный дифференциал. Иногда удается подобрать такую функцию 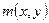, после умножения на которую всех членов уравнения его левая часть становится полным дифференциалом. Общее решение полученного таким образом уравнения совпадает с общим решением первоначального уравнения. Функция 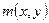называется интегрирующим множителем уравнения (5.1).

Итак, умножим обе части уравнения (5.1) на

.

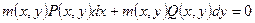(5.1а)

Для того чтобы это уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение

,

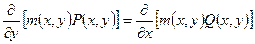т.е. .

Таким образом, интегрирующий множитель есть решение уравнения

.

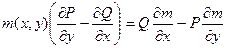(5.6)

В некоторых частных случаях уравнение (5.6) упрощается и интегрирующий множитель для уравнения (5.1) легко найти.

1. Если уравнение (5.1)имеет интегрирующий множитель, зависящий только от х, т.е. 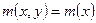, то из уравнения (5.6)имеем

.

(5.7)

2. Если уравнение (5.1) допускает интегрирующий множитель как функцию одной переменной у, т.е. 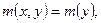то

.

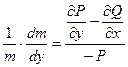(5.8)

Пример 3. Решить уравнение

D Выясним, имеет ли данное уравнение интегрирующий множитель как функцию одной переменой. Вычислим .

,т.е. является функцией, зависящий только от х. Следовательно, интегрирующий множитель находим из уравнения 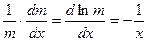, т.е. .

Умножая исходное уравнение на 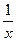, получим уравнение в полных дифференциалах:

.

Записав его в виде ,

имеем Ñ

Лекция 9.

6. Уравнения второго порядка, допускающие понижение порядка

Дифференциальное уравнение второго порядка в общем случае записывается в виде

или, если это возможно, в разрешённом относительно у' ' виде

Общее решение

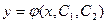
(6.3)

этого уравнения содержит две произвольные постоянные 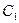и .

Любая функция

(6.4)

получающаяся из общего решения уравнения (6.2) при определённых значениях постоянных 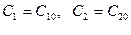, называется частным решением.

Для дифференциальных уравнений второго порядка задача Коши формулируется следующим образом: найти решение у =y (х) уравнения (6.2), удовлетворяющее начальным условиям

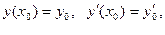
(6.5)

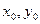y где и 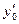– заданные числа.

С геометрической точки зрения условия (6.5) означают,

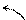
что из семейства интегральных кривых, проходящих

через точку 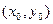, мы выделяем определённую

интегральную кривую, имеющую

заданный угол наклона . y₀

x₀ x

Рассмотрим простейшие случаи, когда уравнение второго порядка решается с помощью квадратур, т. е. применением операций неопределённого интегрирования.

а) y'' = f (x) (6.6)

Полагаем y'=p (x); тогда y''=p', и уравнение (6.6) примет вид p'=f (x), или dp= f (x) dx. Отсюда

p= 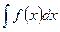=F (x) + C ₁,

где F (x) - первообразная для функции f(x). Так как p=y', то y' = F (x) + C _1, или dy=F (x) dx+C ₁ dx.

Интегрируя ещё раз, находим общее решение уравнения (6.6)

y= +C ₁ x +C ₂.

Пример 1. Найти общее решение уравнения y'' = cos 2 x.

D Положим y '=p (x); тогда y'' =p', следовательно,

p'= cos2 x или dp= cos 2 x dx.

Интегрируя это уравнение, находим

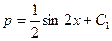или 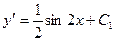, т.е. .

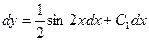Интегрируя второй раз, находим искомое общее решение:

,

т.е. 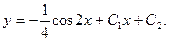Ñ

б) y '' = f (y) (6.7)

Для решения этого уравнения снова полагаем 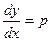, но теперь мы будем считать p функцией от у (а не от ).

Тогда .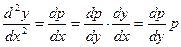

Относительно вспомогательной функции р получаем уравнение первого порядка

.

Интегрируя его, найдём р как функцию от у и произвольной постоянной :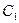

.

Так как 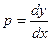, то предыдущее уравнение можно записать так:

.

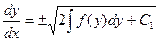Далее, разделяя еще раз переменные и интегрируя, окончательно будем иметь

.

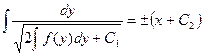Эту формулу общего решения запоминать не следует, нужно усвоить изложенный способ интегрирования.

Пример 2. Проинтегрировать уравнение у''= -у.

D Цепочка преобразований:

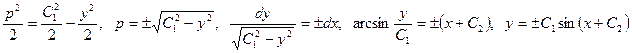Ñ

в) y''=f (y') (6.8)

Полагаем .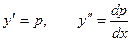

Уравнение (6.8) примет вид .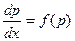

Разделяя переменные и интегрируя, находим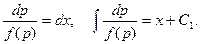

Определив из полученного уравнения величину 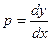путем вторичного интегрирования можно найти .

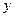Пример 3. Проинтегрировать уравнение .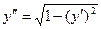

D Цепочка преобразований:

Возвращаясь к переменной 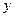, получим Ñ

Итак, в рассмотренных простейших случаях удаётся свести дифференциальное уравнение второго порядка к уравнению первого порядка, введя в качестве новой неизвестной функции производную

Переходим к рассмотрению двух видов уравнений, частными случаями которых являются уравнения (6.7) и (6.8).

Date: 2015-09-02; view: 717; Нарушение авторских прав