Линейное дифференциальное уравнение первого порядка имеет вид

,

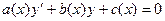(4.1)

где 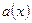, , 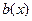c(x) – непрерывные функции.

Если 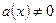, то уравнение (4.1) можно записать в приведённом виде

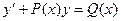
(4.1a)

Здесь 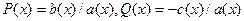– свободный член, называемый также правой частью уравнения. В этом виде будем рассматривать линейное уравнение в дальнейшем.

Если 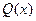¹0, то уравнение (4.1а) называется линейным неоднородным. Если же 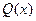º 0, то уравнение принимает вид

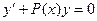
(4.2)

и называется линейным однородным.

Название уравнения (4.1а) объясняется тем, что неизвестная функция y и её производная 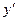входят в него линейно, т.е. в первой степени.

В линейном однородном уравнении переменные разделяются. Переписав его в виде 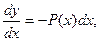откуда 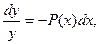и интегрируя, получаем: 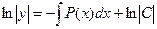,т.е.

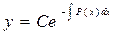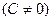
(4.3)

При делении на 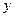теряем решение . Однако оно может быть включено в найденное семейство решений (4.3), если считать, что С может принимать и значение 0.

Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций от х:

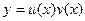
(4.4)

Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).

Дифференцируя обе части равенства (4.4), находим .

Подставляя полученное выражение производной 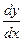, а также значение у в уравнение (4.1а), получаем 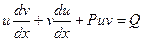, или

.

(4.5)

Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы

,

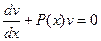(4.6)

т.е. в качестве функции v возьмём решение однородного линейного уравнения (4.6):

.

(4.3а)

Ввиду произвольности в выборе v, мы можем не учитывать произвольную постоянную С (точнее – можем приравнять её нулю). Подставляя найденное значение v (x) в уравнение (4.5), получим, учитывая (4.6):

,

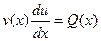(4.7)

откуда

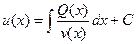
(4.8)

(Здесь C писать обязательно, иначе получится не общее, а частное решение).

Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).

Подставляя 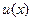и v (x) в формулу (4.4), окончательно получаем

,

или

.

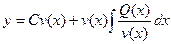(4.9)

Пример 1. Найти общее решение уравнения

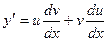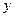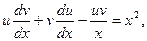D Положим , тогда . Подставляя выражения и в исходное уравнение, получим или (*)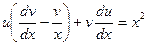

Приравняем нулю коэффициент при :

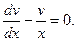
Разделяя переменные в полученном уравнении, имеем 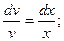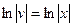(произвольную постоянную C не пишем), отсюда v=x. Найденное значение v подставляем в уравнение (*):

, , .

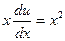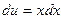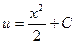Следовательно, общее решение исходного уравнения. Ñ

Отметим, что уравнение (*) можно было записать в эквивалентном виде:

.

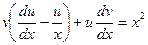Произвольно выбирая функцию u, а не v, мы могли полагать 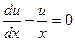. Этот путь решения отличается от рассмотренного только заменой v на u (и, следовательно, u на v), так что окончательное значение у оказывается тем же самым.

На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.

1. Приводим рассматриваемое уравнение к виду .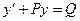

2. Используя подстановку , находим и подставляем эти выражения в уравнение.

3. Группируем члены уравнения, выносим одну из функций u или v за скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.

4. Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.

5. Записываем общее решение, подставив выражения для найденных функций u и v в равенство .

6. Если требуется найти частное решение, то определяем С из начальных условий и подставляем в общее решение.

Отметим далее, что иногда уравнение первого порядка становится линейным, если у считать независимой переменной, а x – зависимой, т.е. поменять роли x и y. Это можно сделать при условии, что x и dx входят в уравнение линейно.

Пример 2. Решить уравнение .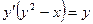

D По виду это уравнение не является линейным относительно функции у.

Однако если рассматривать x как функцию от у, то, учитывая, что ,его можно привести к виду

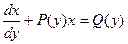
(4.1 б)

Заменив 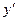на 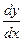,получим 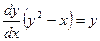или 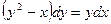. Разделив обе части последнего уравнения на произведение ydy, приведем его к виду

, или . (**)

Здесь P(y)= , . Это линейное уравнение относительно x. Полагаем 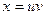, . Подставляя эти выражения в (**), получаем

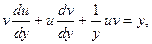или .

Выберем v так, чтобы 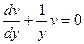, , 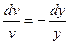откуда ; . Далее имеем , , .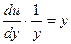

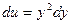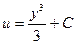Т.к. 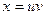, то приходим к общему решению данного уравнения в виде

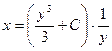. Ñ

Отметим, что в уравнение (4.1а) P (x) и Q (x) могут входить не только в виде функций от x, но и констант: P=a, Q=b. Линейное уравнение

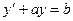
(4.10)

можно решать и с помощью подстановки y= uv и разделением переменных:

; .

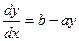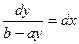Отсюда ; ; 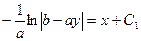; где 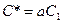. Освобождаясь от логарифма, получаем общее решение уравнения

(здесь ).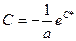

При b= 0 приходим к решению уравнения

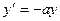
(4.10а)

в виде

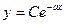
(4.11)

(см. уравнение показательного роста (2.4) при ).

Применим далее для интегрирования неоднородного линейного уравнения (4.1а) метод вариации произвольной постоянной (метод Лагранжа).

Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель С в (4.3) функцией от х, т.е. по существу делаем замену переменной

,

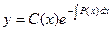(4.3а)

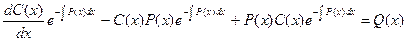где C (x)-новая неизвестная функция x. Подставляя производную в исходное неоднородное уравнение (4.1а), получим: , или

,

(4.12)

откуда, интегрируя, находим

dx+C1,

(4.13)

где С ₁-постоянная. Следовательно,

.

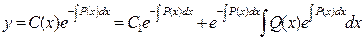(4.14)

Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).

При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).

Применим метод Лагранжа к уравнению, рассмотренному в примере 1:

.

Интегрируем соответствующее однородное уравнение .

Разделяя переменные, получаем 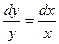и далее 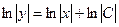. Решение выражения формулой y = Cx. Решение исходного уравнения ищем в виде y = C (x) x. Подставив это выражение в заданное уравнение, получим 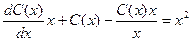; ; 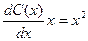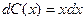, . Общее решение исходного уравнения имеет вид

.

В заключение отметим, что к линейному уравнению приводится уравнение Бернулли

, ()

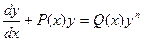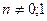(4.15)

которое можно записать в виде

.

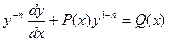(4.15а)

Заменой оно приводится к линейному уравнению:

, , .

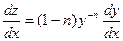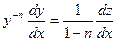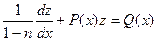Уравнения Бернулли также решаются изложенными выше методами.

Пример 3. Найти общее решения уравнения .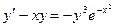

D Цепочка преобразований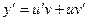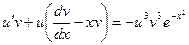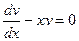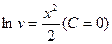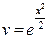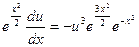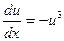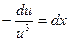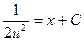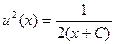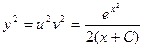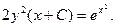: , , , , , , , , , , , , , , Ñ

Date: 2015-09-02; view: 485; Нарушение авторских прав