
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

И наименьшее значение функций на промежутке
|
|
Всюду далее функция f (x) определена на рассматриваемых промежутках.
Теорема 1 (достаточное условие монотонности). Дифференцируемая на (a, b) функция возрастает (убывает) на этом интервале тогда и только тогда, когда 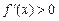
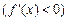
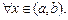
Точка х 0 называется точкой локального максимума (минимума) функции f (x), если существует некоторая окрестность точки  такая, что для всех x из этой окрестности выполняется неравенство
такая, что для всех x из этой окрестности выполняется неравенство 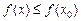

Значение 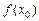 называется локальным максимумом (минимумом) функции.
называется локальным максимумом (минимумом) функции.
Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.
Теорема 2 (необходимое условие существования экстремума функции). Если в точке  функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
Те точки из области определения функции f (x), в которых производная функции f (x) обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того чтобы определить точки экстремума, используют достаточные условия (признаки экстремума).
Теорема 3 (первый признак экстремума функции). Пусть  – критическая точка непрерывной функции f (x). Если в некоторой окрестности точки
– критическая точка непрерывной функции f (x). Если в некоторой окрестности точки  выполняется условие
выполняется условие
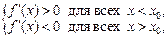
то  – точка локального максимума;
– точка локального максимума;
если выполняется условие

то  – точка локального минимума.
– точка локального минимума.
Если производная 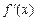 имеет один и тот же знак в левой и правой полуокрестности точки
имеет один и тот же знак в левой и правой полуокрестности точки 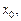 то
то  не является точкой экстремума.
не является точкой экстремума.
Теорема 4 (второй признак экстремума функции). Пусть  – критическая точка дважды дифференцируемой функции f (x). Тогда
– критическая точка дважды дифференцируемой функции f (x). Тогда  является точкой локального минимума функции f (x), если
является точкой локального минимума функции f (x), если 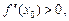 и точкой локального максимума, если
и точкой локального максимума, если 
Теорема 5 (третий признак экстремума функции). Пусть f (x) – n раз непрерывно дифференцируемая в критической точке  функция и
функция и 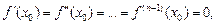
 Тогда:
Тогда:
1) если n – четное и 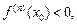 то
то  – точка локального максимума;
– точка локального максимума;
2) если n – четное и  то
то  – точка локального минимума;
– точка локального минимума;
3) если n – нечетное, то  не является точкой локального экстремума.
не является точкой локального экстремума.
З а м е ч а н и е 1. При исследовании функции и построении ее графика целесообразно использовать первый признак экстремума, так как одновременно получаем возможность исследования функции на монотонность.
Точка  называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство
называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство 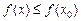

Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).
Теорема 6 (Вейерштрасса). Если функция f (x) непрерывна на отрезке, то она достигает на нем своих наименьшего и наибольшего значений.
Непрерывная на отрезке функция достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.
Для отыскания глобального экстремума функции f (x) на отрезке [ a, b ] необходимо:
1) найти производную 
2) найти критические точки функции;
3) найти значения функции на концах отрезка, т. е. f (a) и f (b), а также в критических точках, принадлежащих (a, b);
4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.
График функции  называется вогнутым (выпуклым вниз) на (a, b), если дуга кривой
называется вогнутым (выпуклым вниз) на (a, b), если дуга кривой  на этом интервале расположена выше любой касательной, проведенной к графику этой функции (рис. 17.1).
на этом интервале расположена выше любой касательной, проведенной к графику этой функции (рис. 17.1).
 |
Рис. 17.1
График функции  называется выпуклым (выпуклым вверх) на (a, b), если дуга кривой
называется выпуклым (выпуклым вверх) на (a, b), если дуга кривой  на этом интервале расположена ниже любой касательной, проведенной к графику этой функции (рис. 17.2).
на этом интервале расположена ниже любой касательной, проведенной к графику этой функции (рис. 17.2).
 |
Рис. 17.2
Теорема 7. Если функция f (x) дважды дифференцируема на (a, b) и 
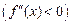 всюду на этом интервале, то график функции вогнутый (выпуклый) на (a, b).
всюду на этом интервале, то график функции вогнутый (выпуклый) на (a, b).
Точка  такая, что график функции
такая, что график функции  меняет выпуклость на вогнутость или наоборот, проходя через
меняет выпуклость на вогнутость или наоборот, проходя через 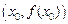 , называется точкой перегиба (рис. 17.3).
, называется точкой перегиба (рис. 17.3).
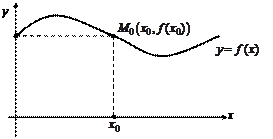 |
Рис. 17.3
Для нахождения точек перегиба вначале находят критические точки 2-го рода – те значения x, для которых 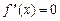 или
или 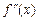 не существует. Далее используют достаточные условия перегиба.
не существует. Далее используют достаточные условия перегиба.
Теорема 8 (первый признак перегиба). Если функция f (x) непрерывна в критической точке 2-го рода  и ее вторая производная
и ее вторая производная 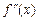 имеет различные знаки слева и справа от
имеет различные знаки слева и справа от 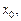 то
то  – точка перегиба.
– точка перегиба.
Теорема 9 (второй признак перегиба). Если функция f (x) имеет непрерывную производную 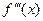 в точке
в точке 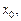 в которой
в которой 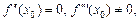 то
то  – точка перегиба.
– точка перегиба.
З а м е ч а н и е 2. При исследовании функции и построении ее графика целесообразно использовать первый признак перегиба, так как одновременно получаем возможность исследования графика функции на выпуклость и вогнутость.
План исследования функции и построения графика
1. Найти область определения D (f) функции f (x).
2. Найти область значений E (f) (если это возможно вначале, часто E (f) можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. Исследовать функцию на периодичность.
5. Найти точки пересечения с осью Ox (нули функции) и точки пересечения с осью Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать функцию на непрерывность, дать классификацию разрывов.
8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).
9. Исследовать функцию на монотонность и экстремум.
10. Исследовать график функции на выпуклость, вогнутость, перегиб.
11. Построить график функции.
Пример 1. Найти экстремумы функции 
Решение. Подозрительными на экстремумы точками будут те, в которых производная функции либо равна нулю, либо не существует.
Найдем производную функции:
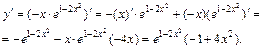
Она определена для любого 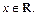
Приравняем производную к нулю:
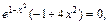 значит,
значит, 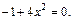 Решая это уравнение, получим
Решая это уравнение, получим 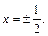 Областью определения функции является числовая прямая.
Областью определения функции является числовая прямая.
Исследуем функцию на экстремум в этих точках тремя способами.
1-й способ. Воспользовавшись теоремой 3, исследуем поведение функции на промежутках 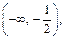
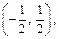
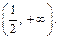
Для этого определим знак производной, т. е. выражения  Очевидно, что для всякого
Очевидно, что для всякого 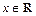 выполняется неравенство
выполняется неравенство  Поэтому знак выражения
Поэтому знак выражения 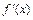 зависит от знака квадратичного выражения
зависит от знака квадратичного выражения 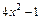 (рис. 17.4).
(рис. 17.4).
 |
Рис. 17.4
Так как при «переходе» через точку с абсциссой  производная
производная 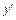 меняет знак с «+» на «–», то, согласно теореме 1, в этой точке функция достигает максимума.
меняет знак с «+» на «–», то, согласно теореме 1, в этой точке функция достигает максимума.
При «переходе» через точку 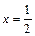 производная
производная 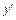 меняет знак с «–» на «+». Поэтому в данной точке функция достигает минимума.
меняет знак с «–» на «+». Поэтому в данной точке функция достигает минимума.
2-й способ. Воспользуясь теоремой 4, вычислим вторую производную функции:

Вычислим ее значение в критических точках  и
и 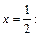
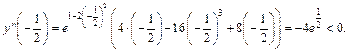
Согласно теореме 4, в точке 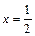 функция достигает максимума.
функция достигает максимума.

Согласно теореме 4 в точке 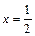 функция достигает минимума.
функция достигает минимума.
3-й способ. Воспользуемся теоремой 5. Так как производная первого порядка в точке  равна нулю, а производная второго (четного) порядка в этой точке меньше нуля, то, согласно теореме 5,
равна нулю, а производная второго (четного) порядка в этой точке меньше нуля, то, согласно теореме 5,  – точка локального максимума. В точке
– точка локального максимума. В точке 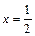 производная первого порядка также равна нулю, а производная второго (четного) порядка больше нуля. Следовательно, точка
производная первого порядка также равна нулю, а производная второго (четного) порядка больше нуля. Следовательно, точка 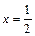 – точка локального минимума.
– точка локального минимума.
Вычислим максимум и минимум функции.
Максимум функции равен значению функции в точке 
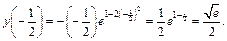
Итак, локальный максимум функции равен 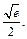
Вычислим значение функции в точке 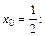

Итак, локальный минимум функции равен 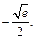
Пример 2. Найти наибольшее и наименьшее значения функции  на отрезке [– 2, 2].
на отрезке [– 2, 2].
Решение. Найдем точки, которые будут подозрительными на экстремум. Для этого вычислим производную функции

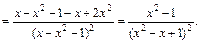
Производная существует во всех точках 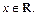 Найдем критические точки. Полагаем
Найдем критические точки. Полагаем 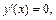 т. е.
т. е. 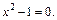 Получаем
Получаем 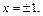 Обе точки
Обе точки 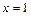 и
и 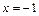 принадлежат интервалу (– 2, 2). Поэтому, будем искать значение функции в этих точках и на концах отрезка. Вычисляем:
принадлежат интервалу (– 2, 2). Поэтому, будем искать значение функции в этих точках и на концах отрезка. Вычисляем:
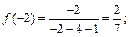

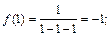
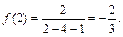
Выбрав среди полученных значений наибольшее и наименьшее, получаем:


Пример 3. Дана функция  Вычислить
Вычислить 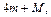 где m и M – соответственно наименьшее и наибольшее значения функции.
где m и M – соответственно наименьшее и наибольшее значения функции.
Решение. Найдем производную функции:
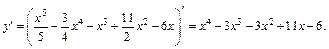
Разложив полученное выражение на множители, получим:
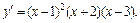
Поскольку функция задана на всей числовой оси (не на отрезке), то исследуем производную на знак методом интервалов (рис. 17.5).
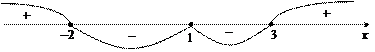
Рис. 17.5
В окрестности точки  выполняется условие
выполняется условие
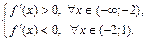
Поэтому, согласно теореме 3 (первый признак экстремума функции),  – точка локального максимума.
– точка локального максимума.
В окрестностях точки 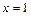 производная
производная 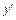 всюду отрицательна. Поэтому в точке
всюду отрицательна. Поэтому в точке 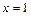 экстремума нет.
экстремума нет.
В окрестности точки 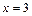 выполняется условие
выполняется условие
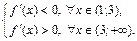
Поэтому 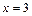 – точка локального минимума.
– точка локального минимума.
Найдем значения функции в точках минимума и максимума:
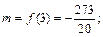
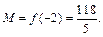
Иных точек локального минимума и максимума функция не имеет.
Искомая величина равна
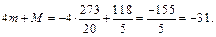
Пример 4. Найти точки перегиба функции 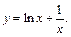
Решение. Для данной функции найдем критические точки 2-го рода. Для этого найдем производную 2-го порядка заданной функции:
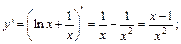
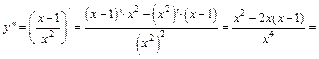
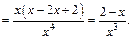
В точке 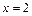 полученная производная
полученная производная 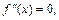 а в точке
а в точке  производная
производная 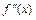 не существует. Поэтому точки
не существует. Поэтому точки 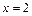 и
и  являются критическими точками 2-го рода.
являются критическими точками 2-го рода.
Исследуем функцию на перегиб несколькими способами.
1-й способ. Воспользуемся теоремой 8 (первым признаком перегиба). Исследуем вторую производную на знак методом интервалов (рис. 17.6).
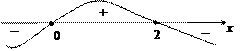
Рис. 17.6
В окрестности точки  выполняется условие:
выполняется условие:
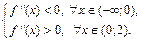
Поэтому, согласно теореме 8,  – точка перегиба функции.
– точка перегиба функции.
В окрестности точки 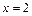 выполняется условие:
выполняется условие:

Поэтому 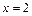 – точка перегиба.
– точка перегиба.
2-й способ: Воспользуемся теоремой 9 (второй признак перегиба). Вычислим:
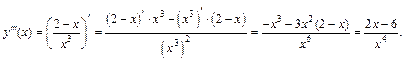
Вычислим значение этой производной в точке 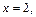 где
где 
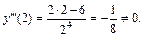
Согласно теореме 9 в точке 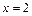 функция имеет перегиб.
функция имеет перегиб.
В точке  заданная функция не определена, однако слева и справа от нее имеет различный характер выпуклости.
заданная функция не определена, однако слева и справа от нее имеет различный характер выпуклости.
Вычислим значение функции в точке 
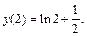
Получили 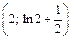 – точка перегиба.
– точка перегиба.
Пример 5. Исследовать функцию 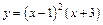 и построить ее график.
и построить ее график.
Решение. Исследование функции произведем согласно указанному выше плану.
1. Область определения функции:
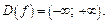
2. Область значений E (f) укажем по результатам исследования.
3. Исследуем функцию на четность и нечетность:
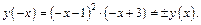
Функция не является четной и нечетной.
4. Функция непериодическая.
5. Найдем точки пересечения графика с координатными осями.
Если у = 0, т. е. 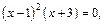 то х = 1, х = –3 – точки пересечения с осью Ох (нули функции).
то х = 1, х = –3 – точки пересечения с осью Ох (нули функции).
Если х = 0, то у = 3 – точка пересечения с осью Оу.
6. Найдем промежутки знакопостоянства функции с помощью метода интервалов (рис. 17.7).
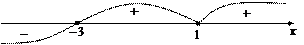 |
Рис. 17.7
Получаем: 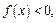 если
если 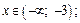
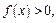 если
если 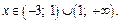
7. Функция непрерывна на всей числовой оси.
8. Горизонтальных асимптот функция не имеет, так как она определена на всей числовой прямой.
Ищем наклонную асимптоту 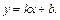

Функция наклонных асимптот также не имеет.
9. Исследуем функцию на монотонность и экстремум. Найдем 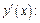
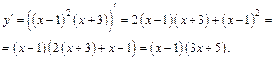
Производная существует 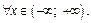 Критическими точками являются те, для которых
Критическими точками являются те, для которых 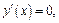 т. е.
т. е. 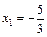 и
и 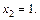
Исследуем знак производной для конкретных промежутков, на которые критические точки делят числовую ось (рис. 17.8).

Рис. 17.8
Согласно теореме 1, функция возрастает на множестве 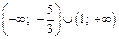 и убывает на
и убывает на 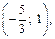 что схематически показано на рис. 17.8. Согласно теореме 3, в точке
что схематически показано на рис. 17.8. Согласно теореме 3, в точке  она имеет локальный максимум, а в точке х = 1 – минимум. Найдем их значения:
она имеет локальный максимум, а в точке х = 1 – минимум. Найдем их значения:
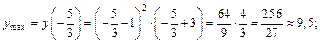
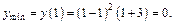
10. Исследуем график функции на выпуклость, вогнутость и перегиб. Вычислим производную 2-го порядка:
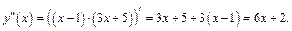
Если 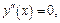 то
то 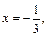 т. е.
т. е.  – критическая точка 2-го рода, иных нет.
– критическая точка 2-го рода, иных нет.
Имеем 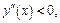 если
если 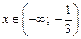 и
и

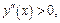 если
если  (рис. 17.9).
(рис. 17.9).
Рис. 17.9
Значит, график функции является выпуклым на 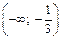 и вогнутым на
и вогнутым на  (согласно теореме 7),
(согласно теореме 7),  – точка перегиба (теорема 8).
– точка перегиба (теорема 8).
11. Используя полученные данные, построим график функции (рис. 17.10).
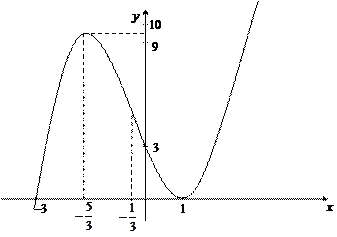 |
Рис. 17.10
Заметим, что 
Пример 6. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. 1. Область определения:

2. Область значений E (f) укажем по результатам исследования.
3. Поскольку область определения D (f) функции не является множеством, симметричным относительно х = 0, то функция не является четной и нечетной.
4. Функция непериодическая.
5. График функции не пересекает ось Ох, так как 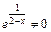 для всех
для всех 
Если х = 0, то 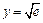 – точка пересечения с осью Оу.
– точка пересечения с осью Оу.
6. Для всех 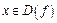 выполняется
выполняется 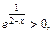 т. е. функция положительна на всей области определения.
т. е. функция положительна на всей области определения.
7. Функция непрерывна на своей области определения, х = 2 – точка разрыва.
Исследуем характер разрыва.
Вычисляем односторонние пределы в точке х = 2:
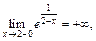
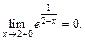
Следовательно, х = 2 – точка разрыва 2-го рода (бесконечный скачок).
8. Найдем асимптоты функции. Поскольку
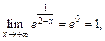

то у = 1 – горизонтальная асимптота.
Мы показали, что в точке х = 2 имеется бесконечный скачок, а поэтому х = 2 – вертикальная асимптота.
Ищем наклонную асимптоту 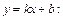

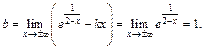
Получаем у = 1 – это горизонтальная асимптота. Наклонных асимптот нет.
9. Исследуем функцию на монотонность и экстремум.
Найдем производную функции:
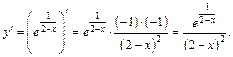
Производная положительна на всей D (f). Следовательно, функция возрастает всюду, где она определена. Экстремума нет.
10. Находим вторую производную:
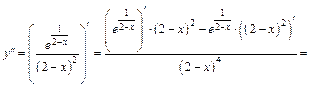
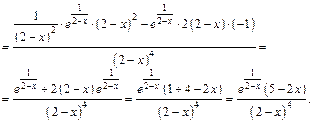
Поскольку 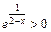 и
и 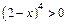 на D (f), то знак производной 2-го порядка зависит от знака выражения 5 – 2 х. Очевидно, что
на D (f), то знак производной 2-го порядка зависит от знака выражения 5 – 2 х. Очевидно, что 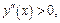 если
если 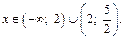 На этих промежутках график функции вогнут.
На этих промежутках график функции вогнут.
Если 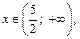 то
то 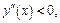 т. е. график функции является выпуклым на этом промежутке. Точка
т. е. график функции является выпуклым на этом промежутке. Точка 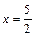 является точкой перегиба, так как при этом значении вогнутость графика изменяется на его выпуклость. Найдем ординату, соответствующую точке перегиба:
является точкой перегиба, так как при этом значении вогнутость графика изменяется на его выпуклость. Найдем ординату, соответствующую точке перегиба:
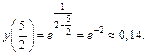
11. Используя результаты исследования, строим график функции (рис. 17.11).
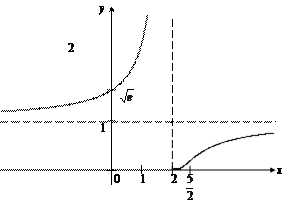 |
Рис. 17.11
В дополнении отметим, что 
Пример 7. Для перевозки груза необходимо изготовить контейнер с крышкой, объем которого равен 72 м3, а стороны основания относятся как 1:2. Определить, каковы должны быть размеры контейнера, чтобы на его изготовление ушло наименьшее количество материала.
Решение. Контейнер представляет собой прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1, объем которого 72 м3 (рис. 17.12).
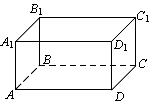 |
Рис. 17.12
Пусть k – коэффициент пропорциональности. Тогда стороны основания равны:
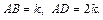
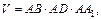 откуда
откуда
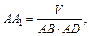 т. е.
т. е. 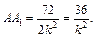
Количество материала, необходимого на изготовление контейнера, численно равно полной поверхности параллелепипеда, т. е. 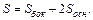
Выразим площадь боковой поверхности:
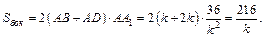
Площадь основания:

Поэтому площадь полной поверхности выражается функцией
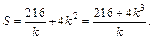
Исследуем полученную функцию на экстремум с помощью первой производной:
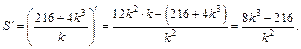
Критические точки: значение k = 0 (производная не существует) – не подходит по смыслу задачи.
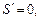 т. е.
т. е. 

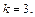
При переходе через точку  производная функции меняет свой знак с «–» на «+». Значит, при
производная функции меняет свой знак с «–» на «+». Значит, при  площадь полной поверхности будет наименьшей. Получаем размеры контейнера:
площадь полной поверхности будет наименьшей. Получаем размеры контейнера:
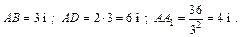
Date: 2015-09-02; view: 550; Нарушение авторских прав