Показательно-степенной функции

Дифференциальное исчисление

Дифференцирование функции с переменной

В основании степени и в показателе

Производная функции

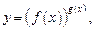(17.1)

где f (x), g (x) – некоторые выражения с переменной x, не может быть вычислена по табличным формулам дифференцирования степенной функции и показательной функции (так как переменная находится как в основании степени, так и в ее показателе).

Заданная функция типа (17.1) называется показательно-степенной.

Способы вычисления производной

показательно-степенной функции

Первый способ. Используют метод логарифмического диф­ференцирования. Для этого:

1) логарифмируют обе части уравнения, которым задается функция (например, по основанию е):

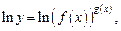
получают

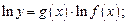
2) дифференцируют обе части полученного равенства, где считают сложной функцией от (правую часть равенства дифференцируют как произведение функций):

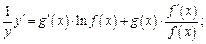
3) выражают из полученного равенства

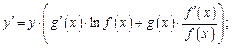
4) заменяют y его выражением через x:

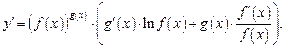(17.2)

При решении данным методом используют не конечную формулу (17.2), а реализуют процесс логарифмического дифференцирования для каждой функции типа (17.1).

Второй способ. На основании свойства логарифмов записывают

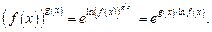(17.3)

Далее дифференцируют как сложную функцию.

С помощью логарифмического дифференцирования удобно также вычислять производные функций при наличии в их аналитическом задании большого количества операций умножения, деления, возведения в степень.

Пример 1. Найти производную функции с помощью логарифмического дифференцирования.

Решение. Функция 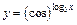является показательно-степенной. Прологарифмируем ее по основанию e:

.

Дифференцируем обе части полученного равенства, учитывая, что y – это функция от x. Используя формулы дифференцирования сложной функции и произведения функций, получаем:

Выразим 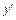из последнего равенства:

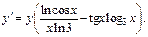
Подставим вместо переменной у заданное выражение и приходим к ответу:

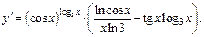
Пример 2. Вычислить производную показательно-степенной функции 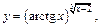используя переход к основанию е.

Решение. Используем формулу (17.3):

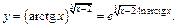
Полученную функцию продифференцируем по правилу вычисления производной сложной функции:

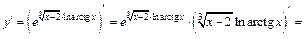
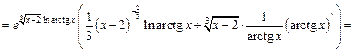
Пример 3. Вычислить значение производной функции в точке

1) 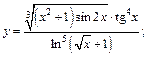2)

Решение. 1) Аналитическое задание данной функции представляет собой выражение, удобное для логарифмирования. Поэтому для нахождения производной этой функции используем метод логарифмического дифференцирования:

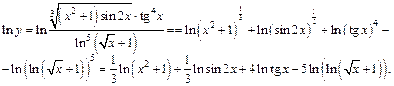
Обе части полученного равенства дифференцируем по переменной х, где считаем сложной функцией от

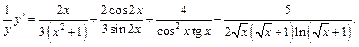
Заменяя у его выражением через х и окончательно преобразуя выражение в правой части, получим:

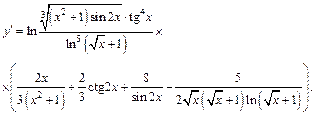
2) Прологарифмируем равенство, задающее функцию по основанию е, используя основные свойства логарифмов:

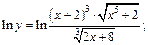
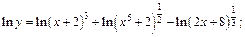
Дифференцируем полученное равенство при условии, что y – это функция от x:

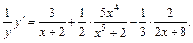
Выразим далее 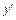и заменим переменную y заданным выражением:

Подставляя в полученное выражение значение 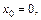получим:

Date: 2015-09-02; view: 729; Нарушение авторских прав