Порядка

Производная определенная на некотором множестве 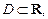является также функцией от x. В случае ее дифференцируемости можно вычислить ее производную. Производная от производной 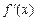называется производной второго порядка:

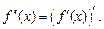
Аналогично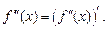

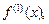
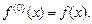Начиная с четвертого, порядок производной обозначают в скобках (сверху): Производные порядка 1–3 также обозначают По определению В случае дифференцируемости производной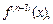 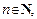производная порядка n определяется равенством

(17.12)

Для производных высшего порядка справедливо свойство линейности:

где 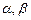– произвольные действительные числа; f (x), g (x) – n раз дифференцируемые функции,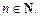

Если f (x) и g (x) – n раз дифференцируемые функции, то верна формула Лейбница:

(17.13)

где – биномиальные коэффициенты: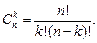

Коэффициенты 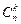можно найти также из треугольника Паскаля.

Если функция у (х) задана в неявном виде уравнением 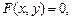то для нахождения производной второго порядка (в случае ее существования) надо продифференцировать найденную первую производную по аргументу x, продолжая рассматривать y как функцию от x. Затем вместо надо подставить найденное ранее значение.

Если функция задана параметрически в виде

то находят вначале производную 1-го порядка по формуле (17.6) и записывают:

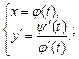(17.14)

Для нахождения производной второго порядка используют формулу (17.6) к параметрически заданной функции (17.14):

Аналогично реализуют тот же подход при нахождении производной 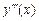и т. д.

Дифференциал от дифференциала функции f в точке x (если функция определена и дважды дифференцируема) называется дифференциалом второго порядка:

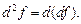
Дифференциал n -го порядка функции f (x) (в случае дифференцируемости n раз, 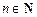) определяют как дифференциал от дифференциала (n –1)-го порядка:

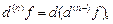
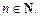
Для вычисления дифференциала порядка n используют формулу

(17.15)

Дифференциалы второго и выше порядков не обладают (в отличие от дифференциалов первого порядка) свойством инвариантности, т. е. их форма, а следовательно, и способ вычисления зависят от того, является ли аргумент x независимой переменной или дифференцируемой функцией другой переменной.

Пример 1. Вычислить 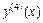для функции:

1) 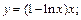2)

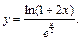
Решение. 1) Вычислим искомую производную последовательно, не применяя формулу Лейбница:

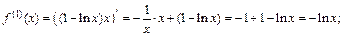
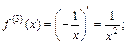
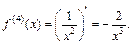
2) Искомую производную удобно найти, используя формулу Лейбница (17.13). Для производной 4-го порядка формула Лейбница примет вид:

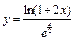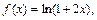
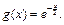Функцию представим в виде Введем обозначения: Для функции f (х) найдем производные:

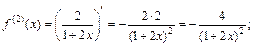
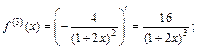
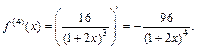
Аналогично для функции g (x) найдем производные:

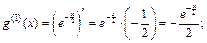
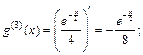
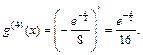
Полученные выражения подставим в формулу Лейбница:

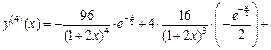
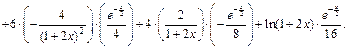
Упрощая это выражение, окончательно получим:

Пример 2. Для функции найти формулу производной n -го порядка, 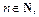если:

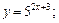1) 2)

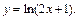
Решение. 1) Вычислим производную 1-го порядка:

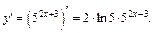
Далее

Установив закономерность, запишем формулу для производной n -го порядка:

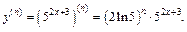
Докажем справедливость этой формулы методом математической индукции.

При имеем 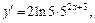что совпадает с найденной ранее производной Предположим, что наша формула верна при 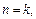т. е.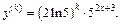

Докажем, что она верна и для 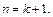Вычислим:

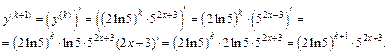
Получили, что равенство выполняется при По методу математической индукции формула будет верна для любого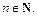

2) Вычисляем последовательно:

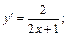
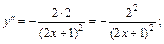
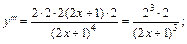
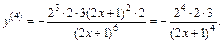
Приходим к заключению, что

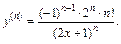
Справедливость этой формулы доказывается методом математической индукции.

Пример 3. Для функции, заданной уравнением 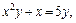найти производную второго порядка.

Решение. Функция задана в неявном виде. Дифференцируем обе части равенства рассматривая y как функцию переменной x:

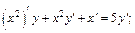
(17.16)

Выражая 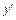из равенства (17.16), получим:

(17.17)

Продолжаем дифференцировать по переменной x равенство (17.16):

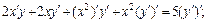
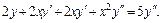
Из последнего равенства выражаем

Подставим в эту формулу найденное выражение (17.17) для 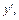получим:

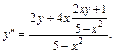
После упрощения приходим к ответу: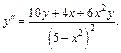

Пример 4. Вычислить 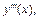если

Решение. По формуле (17.6) получаем

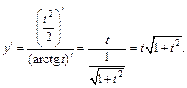
Имеем:

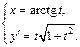
Для нахождения производной второго порядка снова используем формулу (17.6):

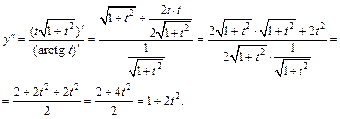
Результат может быть записан в виде

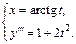(17.18)

Дифференцируем еще раз:

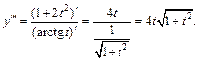
Из первого равенства системы (17.18) можем выразить t через x:

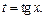
Подставляем полученное выражение в формулу производной третьего порядка и приходим к ответу:

т. е.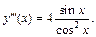

Пример 5. Найти 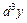для функции

Решение. Согласно формуле (17.15), для дифференциала 3-го порядка справедлива формула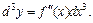

Последовательно вычисляем производные заданной функции:

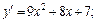
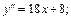
Подставив полученное выражение в формулу приходим к ответу:

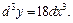
Date: 2015-09-02; view: 362; Нарушение авторских прав