Нечеткое отношение эквивалентности, неэквивалентности, сходства, различия, предпорядка, порядка. Нечеткий гомоморфизм между нечеткими отношениями

Нечеткие отношения эквивалентности

Отношение является нечетким отношением эквивалентности, если для всех его элементов a,b,c A это отношение удовлетворяет следующим свойствам:

1. Рефлексивность Для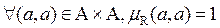

2. Симметричность

3. Max-min-транзитивность для

В соответствии с определением декомпозиции нечеткое отношение эквивалентности мб представлено в виде совокупностей альфа-уровней этого отношения.

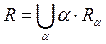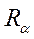, - значение альфа-уровня нечеткого отношения, 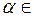уровневому множеству

Нечеткое отношение эквивалентности задает иерархическую совокупность разбиения множества А на непересекающиеся классы эквивалентности.

В практических задачах нечеткое отношение эквивалентности можно получить из нечеткого нетранзитивного отношения сходства применяя операцию транзитивного замыкания.

Нечеткое отношение неэквивалентности.

R_нэ двойственно нечеткому отношению эквивалентности R_э, т.е. одно может быть получено из другого с использованием операции дополнения.

Для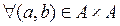

Определение

Отношение R_нэ является нечетким отношением неэквивалентности (ультраметрика), если для всех элементов a,b,c, принадлежащих А, оно удовлетворяет следующим 3 свойствам:

1) Антирефлексивность

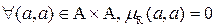
2) Симметричность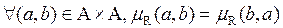

3) Max-min-транзитивность для

Для нечеткого отношения неэквивалентности двойственным образом вводится понятие транзитивного замыкания

k-степень соответствия нечеткого отношения, n-число элементов множества А

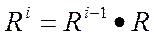
-операция min_max композиции

Нечеткие отношения сходства

Отношение R является нечетким отношением сходства или толерантности, если для всех a,b принадлежащих А оно удовлетворяет следующим двум условиям:

1.Рефлексивность Для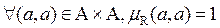

2.Симметричность

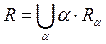
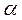-само значение альфа-уровня

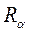- отношения альфа-уровня

Эти альфа-уровни определяют покрытие множества элементов А классами сходства.

В отдельный подкласс нечетких отношений сходства могут быть выделены отношения, обладающие помимо свойств рефлексивности и симметричности специфическими свойствами транзитивности, получающимися заменой операции min на другие операции умножения.

Можно заменить min на Произведение (* 1) или граничное произведение (это будет отношением сходства)(*2)

Нечеткое отношение различия

R-несходства

Для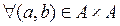

Отношение R является нечетким отношением различия, если оно удовлетворяет следующим свойствам:

1) Антирефлексивность

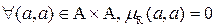
2) Симметричность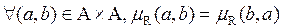

В отдельный подкласс нечетких отношений различия (несходства) могут быть выделены отношения, обладающие помимо свойств антирефлексивности и симметричности свойствами транзитивности, двойственным свойствам (*1 и *2).

Двойственность проявляется в том, что для этих операций транзитивности знак >= заменяется <=.

Операция max заменяется на min.

Операции произведения или граничного произведения заменяются суммой или граничной суммой.

Отношение эквивалентности и неэквивалентности –двойственное отношение.

Нечеткие отношения порядка.

Отношение 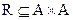является нечетким нестрогим отношением порядка, если и удовлетворяет следующим свойствам:

1. Рефлексивность

2. Антисимметричность: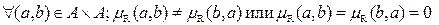

3. 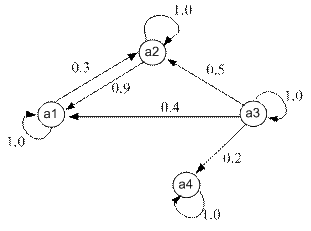Max-min-транзитивность:

Введем понятие соответствующего четкого порядка.

Он образуется на основе соответствующего нечеткого порядка на основе следующих преобразований:

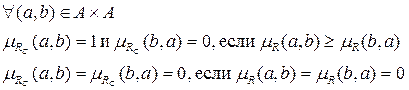
Если отношения соответственного четкого порядка, нечеткого отношения порядка представляет собой общий или линейный порядок, то нечеткое отношение называется нечетким общим порядком, если нет, то нечеткое отношение называется нечетким частичным порядком.

Если условие рефлексивность заменить на условие антирефлексивности, то нечеткое отношение будет называться нечетким отношением строгого порядка.

Если условие антисимметричности заменяется на совершенную антисимметричность, то отношение порядка трансформируется в совершенное антисимметричное отношение порядка.

Совершенная антисимметричность:

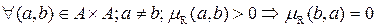
Введем понятие доминирования:

Если в нечетком отношении порядка, заданном на отношении А, и 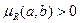, то говорят что a доминирует над b. При этом все элементы образуют доминирующий класс над элементом а 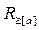, а все элементы b из А для которых образуют доминируемый класс .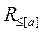

Для элемента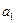

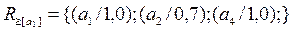
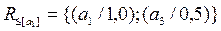
Отношение нечеткого предпорядка.

Это отношение , , 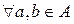удовлетворяет следующим свойствам:

1. Рефлексивность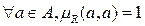

2. max-min-транзитивность

Date: 2015-08-24; view: 1405; Нарушение авторских прав