Реализация электронных и туннельных переходов. Метод Монте-Карло

Электронные и туннельные переходы в ЭК-модели можно представить в терминах дискретного марковского процесса с различными вероятностями переходов между состояниями марковской цепи. Для описания случайных марковских процессов обычно используют метод Монте-Карло, который заключается в применении генератора псевдослучайных чисел для моделирования случайного процесса переходов между состояниями.

Простейшим способом описания инактивационного состояния является введение новой переменной μ, принимающей два значения: μ= 1, если канал инактивирован, μ= 0 в остальных случаях. Если ввести функцию Хэвисайда 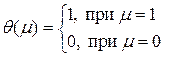, то с учетом новой переменной адиабатический конформационный потенциал (2.4) имеет следующей вид:

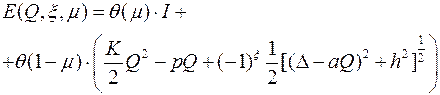, (2.32)

где 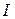– энергия инактивационного состояния.

Диабатический конформационный потенциал (2.5) может быть описан следующей формулой:

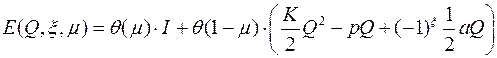. (2.33)

Для инактивационного состояния, была введена новая переменная μ.

Рассмотрим состояние канала 1: 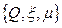в определенный момент времени 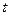. В следующий момент времени 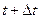система может оказаться в состояниях 2: 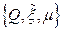или 3: 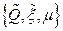или 4: (рис. 2.15).

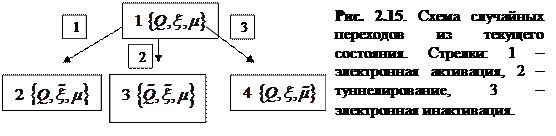
Предполагается, что потоки событий электронных и туннельных переходов между состояниями являются пуассоновскими. Опираясь на это предположение, дискретизируем марковский процесс с таким малым шагом по времени 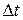, что за этот промежуток времени может произойти только одно событие перехода.

На каждом шаге интегрирования случайного процесса вероятности туннельного, электронного перехода между ветвями КП и вероятность перехода в инактивационное состояние определялись следующим образом:

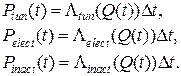(3.34)

Так как события туннельных и электронных переходов являются независимыми, то вероятность покинуть состояние 1 за время 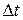равна .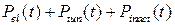

Однако для построения цепи нужно знать еще вероятности переходов в «состояние 2» и «состояние 3» при условии, что канал покинет «состояние 1». Эти вероятности могут быть вычислены по следующим формулам:

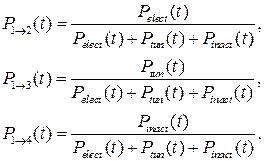(2.35)

В данной работе предполагается, что при осуществлении быстрых переходов не происходит изменения конформационной координаты по уравнению Ланжевена. Медленная конформационная динамика в течение промежутка времени 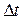реализуется только в отсутствии быстрых переходов.

На основе сделанных предположений была получена марковская цепь, которая реализовывалась с помощью метода Монте-Карло. В рамках этого метода нормально распределенная случайная величина 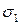задается на i -том шаге реализации процесса в момент времени 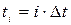на отрезке [0,1] и сравнивается с вычисленной вероятностью электронных переходов между ветвями КП. Если выполняется условие 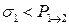, реализуется электронный переход между ветвями КП. В ином случае определялась следующая случайная величина 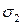, которая сравнивалась с условной вероятностью туннельного перехода. По аналогии с предыдущим случаем, если 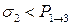, то реализуется туннельный переход, в другом случае определяется случайная величина 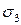. При 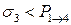моделируется инактивационный переход, в противном случае вычисляется конформационная координата на текущем шаге по уравнению Ланжевена.

Повторяя описанную процедуру 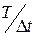раз, где Т – длительность эксперимента, и вычисляя конформационную динамику на отрезках 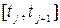, на которых отсутствуют переходы, можно получить одну реализацию случайного процесса, которая является приближением исходного марковского процесса электронных и туннельных переходов.

Date: 2015-08-24; view: 462; Нарушение авторских прав