Анализ временных зависимостей конформационной координаты Q

При проведении численных экспериментов исследовалась динамика одиночного RyR-канала. В начальный момент времени канал находился в электронно- и конформационно-закрытом состоянии. Результаты экспериментов по изучению зависимости конформационной координаты Q от времени обрабатывались с помощью метода нормированного размаха (R/S-анализ или метод Херста) [43, 116].

Этот метод позволяет выявить скоррелированность определенного ряда данных на больших интервалах времени и определить фрактальную размерность временного ряда – размерность Хаусдорфа-Безиковича: 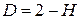, где Н – показатель Херста.

Согласно [116], значения Н>0.5 указывают на положительную корреляцию (персистентный процесс), а Н<0.5 на отрицательную корреляцию (антиперсистентный процесс) измеряемой величины со временем. И тот и другой процессы являются процессами с «памятью», когда последующие события определяются предшествующими. Величина Н=0.5 характеризует случайный процесс.

Среднее значение координаты Q на промежутке времени τ определяется как:

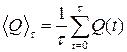, (3.1)

где t – дискретное время с шагом dt. В данной работе dt выбиралось равным 0.05 c, длительность эксперимента: 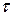=1 с.

Накопившееся отклонение конформационной координаты от среднего значения 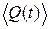определяется как: 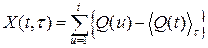. Разность между максимальным и минимальным значениями Q(t) в выборке (кумулятивное отклонение от среднего) на интервале времени τ описывается формулой:

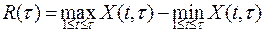, (3.2)

Стандартное отклонение Q(t) от:

. (3.3)

Величина R/S носит название нормированного размаха. Как показал Херст [116], для многих временных рядов наблюдаемый нормированный размах хорошо описывается эмпирическим соотношением: .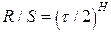

Показатель Херста Н определяется через тангенс наклона прямой 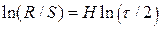, полученной в результате аппроксимации точек прямой методом линейной регрессии в логарифмических координатах. Этот показатель характеризует скоррелированность членов исследуемого ряда.

При анализе результатов численных экспериментов по изучению зависимости Q(t) на интервале времени 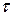, вводилась новая переменная 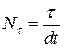– число шагов dt на интервале времени 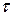. На рисунке 3.3 приведен пример (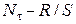)-зависимостей (графиков Херста), построенных в логарифмических координатах, для дискретного временного ряда Q(t) при двух различных значениях параметра эффективного трения Г (рис. 3.3а) и при двух значениях коэффициента упругости канала К (рис. 3.3б).

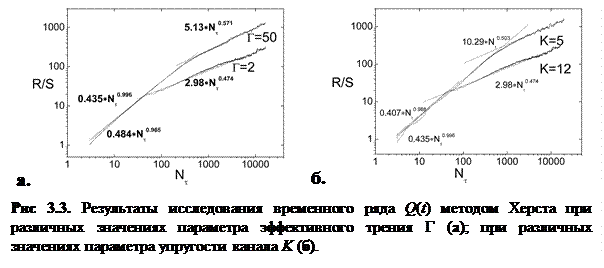
На основании полученных зависимостей можно сделать вывод, что динамика RyR-канала в рамках ЭК-модели является сильно коррелированной (H ≈ 1.0) на относительно коротком промежутке времени, сравнимом с длительностью конформационной релаксации канала в метастабильный минимум потенциала, соответствующий открытому состоянию, и слабо коррелированной на длительных промежутках времени (H ≈ 0.5).

Основываясь на результатах проведенного R/S-анализа, можно заключить, что в рамках электронно-конформационной модели динамика координаты Q канала является не только стохастической, но и детерминированной, причем на коротких интервалах времени, и при этом исследуемая система обладает «памятью».

Следует отметить, что на сегодняшний день в литературе отсутствуют экспериментальные данные, указывающие на фрактальные свойства RyR-каналов, поэтому необходим более детальный экспериментальный анализ конформационных изменений RyR-канала с целью подтверждения результатов, полученных с помощью представленной здесь модели.

Для предсказания поведения исследуемой системы требуется детальный параметрический анализ как медленной конформационной динамики, так и быстрых переходов RyR-канала в рамках ЭК модели.

Date: 2015-08-24; view: 469; Нарушение авторских прав