Сопряжение динамики RyR-каналов с динамикой кальция в отделах высвобождающей единицы

Для создания замкнутой модели высвобождающей единицы с учетом стохастической динамики RyR-каналов была установлена связь между параметрами теории высвобождающей единицы и ЭК-моделью.

В модели высвобождающей единицы поток высвобождающегося Са²⁺ в диадное пространство зависит от числа открытых каналов в кластере.

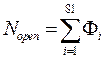, (2.22)

где 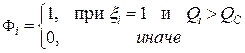– «открытость» канала, где 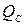– значение конформационной координаты точки локального максимума нижней ветви C конформационного потенциала (3.3.3) (см. рис. 2.3).

Таким образом, динамика концентрации кальция в отделах высвобождающей единицы вызывает изменение параметра 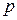, который влияет на динамику состояний RyR-каналов, и как следствие, на число открытых RyR-каналов N_open. Переменная N_open, в свою очередь, определяет скорость высвобождения кальция из люмена СР.

На основе вышеизложенных положений получена замкнутая объединенная модель, на базе которой в данной работе проводилось численное моделирование динамики Са²⁺ в отделах кардиомиоцитов.

2.2.4 Модель Са²⁺-высвобождающей единицы

Разработка модели Са²⁺-высвобождающей единицы основана на широко известной модели структуры клетки (рисунок 2.14) [90, 112, 113], состоящей из четырех основных компонентов: диадного пространства, цитозоля, сети СР и просвета ТЦ (люмена) СР. Особенностью данного представления является рассмотрение обобщенной Са²⁺ высвобождающей единицы.

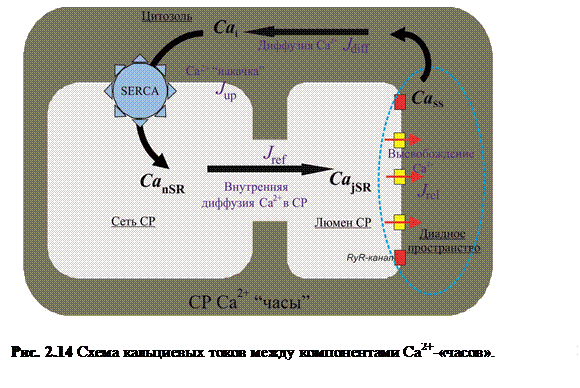
Основываясь на схеме динамики Са²⁺ в клетке, введены четыре кальциевых потока между отделами клетки:

1. Поток заполнения люмена 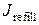(от англ. refill – заполнять), его значение зависит от параметра скорости заполнения 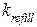и разности концентраций Са²⁺ в сети СР и в люмене и определяется как:

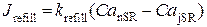. (2.23)

2. Поток высвобождения Са²⁺ из люмена 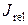(от англ. release – высвобождать), величина которого зависит от числа открытых каналов в кластере высвобождающей единицы 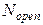и от величины потока Са²⁺ через одиночный открытый канал :

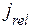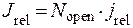. (2.24)

Значение потока Са²⁺ через одиночный канал определяется формулой:

, (2.25)

где – параметр скорости высвобождения, 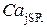– концентрация Са²⁺ в люмене, 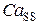– концентрация Са²⁺ в диадном пространстве.

3. Диффузионный поток между диадным пространством и цитозолем , значение которого зависит от градиента концентраций Са²⁺ в диадном пространстве и в цитозоли 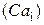и определяется как:

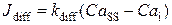, (2.26)

где 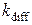– параметр скорости диффузии.

4. Поток заполнения сети СР 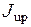(от англ. uptake – накачка). Процесс накачки СР кальцием против градиента концентрации требует энергетических затрат (фосфорилляция молекул АТФ), значение потока зависит от концентрации Са²⁺ в цитозоле и от параметров Са²⁺-насоса: 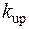(скорость накачки) и 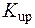(чувствительность насоса). Для зависимости потока от концентрации Са²⁺ была использована формула, заимствованная из модели [54]:

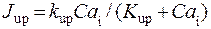. (2.27)

Кальциевые потоки в упрощенной модели сердечной клетки (рис. 2.14) с учётом квазистационарного взаимодействия с кальциевыми буферами описываются стандартной системой дифференциальных уравнений [91]:

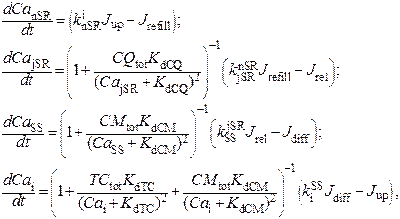(2.28)

В модели учитывается связывание ионов Са²⁺ с регуляторными глобулярными белками – буферами, которые участвуют в процессе мышечного сокращения. Были учтены следующие Са²⁺-связывающие буферы, содержащиеся в кардиомиоците: кальсеквестрин, кальмодулин, тропонин.

Параметры концентраций буферов, учитывающиеся в модели, взяты из работы [85]: CQ _tot = 10^-2 М - полная концентрация кальсеквестрина, CM _tot = 45·10^-6 М - полная концентрация кальмодулина, TC _tot = 31·10^-6 М - полная концентрация тропонина C. 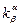- константы отношений объемов 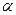и 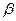отделов клетки (рис. 2.14) ( = 40, 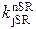= 9.7, 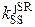= 0.12, 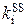= 0.022). 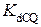= 833·10^{-6 M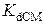}, = 2.4·10^{-6 M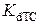}, = 5·10^{-6 M} – константы диссоциации соответствующих буферов. Следует отметить, что все эти параметры выбраны как типичные для интегративной модели, а не для модели одиночной высвобождающей единицы.

Другими словами, было предположено, что все RyR-каналы формируют систему идентичных высвобождающих единиц, функционирующих согласованно. Параметры ЭК модели (2.5, 2.7, 2.8) при проведении численных экспериментов ­имели следующие значения: a = 5, K = 12, 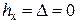, Г = 7. Параметры туннелирования: A = 1, 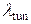= 0.01 [A2].

Date: 2015-08-24; view: 483; Нарушение авторских прав