Стохастическая динамика и электронно-конформационные взаимодействия в белках

Отдельно следует рассмотреть целый класс стохастических моделей динамики белков, и, в частности, ионных каналов, которые основаны на принципах электронных и конформационных взаимодействий в белках [41-46].

Белковые комплексы рассматривается как вязкоупругие объекты [46], обладающие большим количеством степеней свободы.

Перераспределение химических связей в ходе взаимодействия активных центров белковых соединений с ионами изменяет распределение электронной плотности в реагирующих молекулах, изменяя тем самым баланс сил внутри белка, что приводит к тому, что равновесная конформация белка до и после реакции различны. Это явление называется электронно-конформационным взаимодействием, а соответствующее изменение структуры – электронно-конформационным переходом [45, 47]. Этот переход можно также рассматривать и как конформационную релаксацию под действием нескомпенсированных сил, возникающих после акта перераспределения электронной плотности или иных изменений в активном центре белка. Присоединение очень небольшого по размерам иона к активному центру ионного канала вызывает существенные изменения конформации белка – поворот субъединиц на расстояние порядка 10 А. Этот пример показывает, насколько тонким является баланс сил, стабилизирующих конформацию белковой структуры.

Ярким примером являются непрерывные модели, к примеру, модель процессов открытия Са²⁺-активируемых K⁺-каналов [45]. При разработке данной математической модели авторы основывались на ряде важнейших фактов, выявленных экспериментально и характеризующих кинетику активности ионных каналов, таких как:

1) распределение кинетических параметров может иметь не экспоненциальное, а степенное распределение.

2) распределения имеют фрактальную структуру (самоподобны в различных временных масштабах [47, 48]);

3) существует скоррелированность событий ("память") в активности канала [48].

4) кинетика переходов канала между различными состояниями определяется не только случайными, но и детерминированными силами [48].

В модели [41] конформационное состояние канала и, соответственно, его проводимость определялись с помощью введения угла отклонения подвижных трансмембранных сегментов канала от центральной оси поры (рис. 1.17). Предполагалось, что канал при отсутствии внешних воздействий может находиться в двух устойчивых состояниях (открытое и закрытое). Переходы между состояниями осуществляются благодаря воздействию тепловых флуктуаций на подвижные части сегментов. Потенциальная энергия воротного механизма (структуры) описывается функцией с двумя локальными минимумами, соответствующими открытому и закрытому состояниям канала (рис. 1.17г).

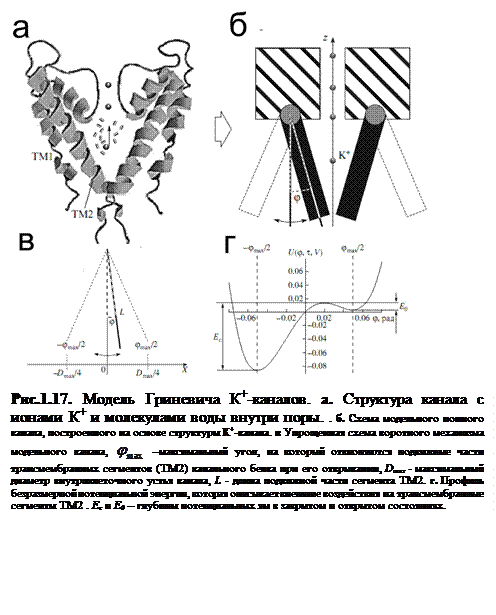
Таким образом, существует альтернатива теориям, основанных на марковских процессах, описывающих процессы открытия/закрытия ионных каналов. Вышеописанные модели позволяют более детально описать динамику биомолекул и предполагают использование энергетического подхода к описанию конформационных изменений различных биофизических объектов.

1.5 Кооперативная динамика группы RyR-каналов. Са²⁺-высвобождающая единица

Начальное возрастание концентрации внутриклеточного кальция в ответ на электрическое возбуждение происходит благодаря поступлению ионов извне через L-каналы, однако такого повышения концентрации недостаточно для сокращения клетки [1, 11, 50, 51]. Внешний приток Са²⁺ активирует группы RyR-каналов, являясь стимулом для последующего высвобождения Са²⁺ из СР и повышения уровня Са²⁺ в цитозоле на порядок величины. Данный триггерный процесс носит название «кальцием вызванное высвобождение кальция» (КВВК) [1]. После высвобождения Са²⁺ из СР в диадное пространство и дальнейшей его диффузии в цитозоль увеличивается концентрация Са²⁺ вблизи миофибрилл, что приводит к сокращению саркомера. Относительная однородность повышения концентрации Са²⁺ в клетке обеспечивается особым устройством СР с небольшим расстоянием (не более 1 мкм) от любой точки клетки до ближайшей высвобождающей единицы [10].

Являясь одним из ключевых процессов электромеханического сопряжения, процесс КВВК требует тщательного экспериментального анализа и соответствующего математического моделирования.

1.6 Локальные высвобождения Са²⁺ в кардиомиоцитах

Важным этапом в исследовании динамики Са²⁺ в кардиомиоцитах являются эксперименты по изучению локальных высвобождений Са²⁺ в клетках при помощи конфокальной микроскопии и Са²⁺-чувствительного индикатора fluo-3, fluo-4, или rhod-2 [51]. Резкое локальное повышение концентрации цитозольного Са²⁺ в покоящейся клетке, называется Са²⁺ спарком [52-54]. Спарки в клетке наблюдаются с частотой около 100 в секунду [53].

На рисунке 1.18 приводятся результаты продольного сканирования сердечной клетки крысы, которая загружена индикатором fluo-3. Каждый Са²⁺ спарк является по форме почти сферическим с приблизительным диаметром 2 мкм. Как видно из рисунка 1.18в, значение концентрации покоя Са²⁺ около 100 нM, а значение локальных пиков концентрации от 200 до 300 нM.

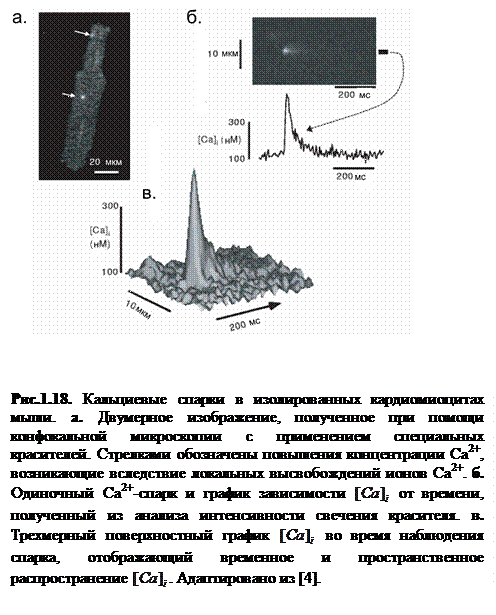
Поскольку Са²⁺ спарки формируются кластерами RyR-каналов, они преимущественно наблюдаются вдоль саркомера и T-тубулы. На рисунке 1.18б представлено усредненное изображение спарков перпендикулярно Т-тубулы.

1.7 Модели «общего пула»

Одной из самых распространенных теорий для описания процесса КВВК на протяжении долгого времени являлась так называемая «теория общего пула» [55-57]. Она основана на усреднении концентрации Са²⁺ в сарколемме и в субклеточных пространствах. В рамках этой модели огромное количество Са²⁺-высвобождающих единиц описывались одной обобщенной модельной высвобождающей единицей. При этом поток Са²⁺ через L-каналы объединен в общий стимулирующий поток, а поток высвобождающегося Са²⁺ – в общий поток высвобождения. Оба этих потока направлены в один обобщенный отдел клетки, называемый субпространством (объединенное диадное пространство), причём процесс высвобождения зависит от концентрации Са²⁺ в субпространстве. Следовательно, однажды запущенное высвобождение Са²⁺ из СР должно повышать концентрацию Са²⁺ в субпространстве по принципу "всё или ничего". Согласно этой модели количество высвободившегося Са²⁺ не зависит от величины стимулирующего мембранного тока, что противоречит экспериментальным данным [58].

С помощью этого обобщения в целом ряде других математических моделей, использующих теорию общего пула, исследователи пытались описать изменение концентрации Са²⁺ внутри клетки в течение сократительного цикла – кальциевый переход. Эти модели опирались на кинетические характеристики процессов накопления Са²⁺ во внутриклеточных структурах и взаимодействие с буферами [59, 60].

Объединение модели общего пула с интегративными моделями кардиомиоцитов позволило с хорошей степенью точности предсказать динамические процессы активности клетки [61].

Однако модель общего пула имеет ряд недостатков. В частности, она не способна описать следующие экспериментальные факты [29-33 ]:

· явление нелинейного усиления отклика высвобождающих структур СР на увеличивающийся приток Са²⁺ извне – явление градуальности.

· эффект быстрого завершения активного высвобождения после исчезновения стимула – termination.

· эффект адаптации высвобождения к повторной стимуляции.

Как уже отмечалось, запуск процесса КВВК в сердечной клетке стимулируется незначительным повышением концентрации Са²⁺ в цитозоле вследствие поступления внеклеточного Са²⁺ через L-каналы [1].

Явление градуальности отклика обнаружено экспериментально и заключается в том, что при увеличении количества Са²⁺, поступающего извне, происходит возрастание количества высвободившегося Са²⁺. Кроме того, отклик высвобождающей системы сильно зависит от скорости повышения стимулирующего Са²⁺ тока [1]. Этот феномен невозможно описать в рамках модели общего пула.

Весте с тем, целый ряд экспериментов указывает на то, что в процессе высвобождения СР после его завершения концентрация Са²⁺ в СР не падает до нулевого уровня [52]. В модели же общего пула высвобождение Са²⁺ завершается при полном опустошении СР по принципу «все или ничего».

Опираясь на данные расхождения, можно сделать вывод о неспособности модели общего пула с хорошей точностью описать динамические процессы ионов Са²⁺ в кардиомиоците.

Date: 2015-08-24; view: 784; Нарушение авторских прав