Атты дененің тұрақты өсті айнала қозғалуы

Қозғалыстағы дененің кем дегенде екі нүктесі (А және В) қозғалмайтын болса, онда қозғалыс қатты дененің тұрақты өсті айнала қозғалуы деп аталады (2-сурет). Қозғалмайтын екі нүктені қосатын түзу айналу өсі деп аталады. Айналу өсінде жататын нүктелердің барлығы қозғалмайды.

Ал айналу өсінде жатпайтын нүктелер центрлері айналу өсінде жататын, жазықтықтары айналу өсіне перпендикуляр шеңберлер сызады.

Дененің мұндай қозғалысын бір параметрмен, яғни оның 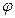айналу бұрышымен сипаттауға болады. Егер денені айналу өсі арқылы өтетін қозғалмайтын (1) және денемен бірге қозғалатын (2) жазықтықтармен қисақ (2-сурет), осы жазықтықтар арасындағы екі жақты бұрышдененің айналу бұрышы деп аталады. Енді айналу өсінің бойымен Oz өсін бағыттаймыз. Сонда Oz өсінің ұшынан қарағандағы 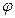айналу бұрышының сағат тіліне қарсы бұрылу бағытын оң бағыт деп аламыз.

Дененің тұрақты өсті айналу заңы былай жазылады:

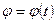, (2)

мұндағы j - дененің айналу бұрышы. Айналу бұрышы 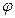радианмен өлшенеді.

Қатты дененің айналмалы қозғалысының негізгі кинематикалық сипаттамаларына бұрыштық жылдамдық пен бұрыштық үдеу жатады. Бұл ұғымдарды енгізу үшін дене 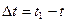уақытта Dj бұрышқа бұрылды деп санаймыз (3-сурет). Сонда Dj - дің Dt - ға қатынасы Dt уақыттағы дененің орташа бұрыштық жылдамдығы деп аталады:

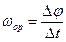. (3)

Dt нөлге ұмтылғандағы бұл қатынастың шегін дененің бұрыштық жылдамдығының алгебралық мәні деп атайды:

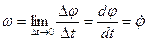. (4)

Сонымен, дененің бұрыштық жылдамдығының алгебралық шамасы айналу бұрышынан уақыт бойынша алынған бірінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық жылдамдығы деп атаймыз:

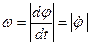. (5)

Радиан өлшемсіз бірлік болғандықтан, бұрыштық жылдамдықтың өлшем бірлігі ретінде рад/с немесе 1/с 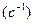қолданылады.

Дәл осылай дененің орташа бұрыштық үдеуін аламыз:

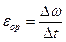, (6)

ал бұрыштық үдеудің алгебралық мәні мынандай:

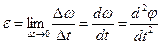немесе 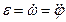. (7)

Сонымен, дененің бұрыштық үдеуінің алгебралық шамасы бұрыштық жылдамдықтың алгебралық шамасынан уақыт бойынша алынған бірінші туындыға немесе айналу бұрышынан алынған екінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық үдеуі дейтін боламыз:

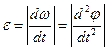немесе 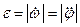(8)

Бұрыштық үдеудің өлшем бірлігі рад/с² немесе 1/с².

Техникалық есептеулерде көбіне бұрыштық жылдамдықтың орнына n – дененің минутына жасайтын айналу саны, ал айналу бұрышының орнына N – айналу саны жиі қолданылады. Дене бір айналғанда 2p бұрышқа бұрылады, ал бір минутта 60 секунд бар екенін ескерсек, бұл шамалардың арасындағы байланыстар:

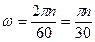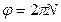және (9)

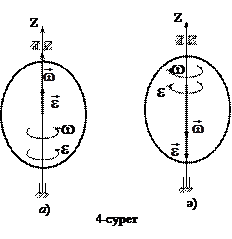
Енді бұрыштық жылдамдық пен бұрыштық үдеу векторларының ұғымын ендіреміз. Бұл векторлардың модульдері (5) және (7) өрнектерімен анықталады, ал бағыттары олардың алгебралық мәндері (w мен e) нөлден үлкен болса айналу өсінің бойымен оң бағытта (4 а -сурет), нөлден кіші болса – теріс бағытта (4 ә) сурет) бағытталады. Бұл жерде 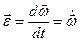. Егер бұл векторлар бір бағытта болса дененің айналуы үдемелі, ал қарсы бағытта болса – кемімелі деп аталады.

Суретте бұрыштық жылдамдық пен бұрыштық үдеу векторларын доға тілімен де бейнелейді. Олардың алгебралық мәндерінің таңбасы оң болса Oz өсінің ұшынан қарағанда доға тілдері сағат тіліне қарсы, ал теріс болса – сағат тілімен бағыттас (4-сурет) бағытталады.

Date: 2015-09-03; view: 1716; Нарушение авторских прав