Нүкте қозғалысының кейбір дербес жағдайлары

Нүкте қозғалысының кейбір дербес жағдайларын қарастырып, олардың негізгі кинематикалық сипаттамаларын анықтайық.

1. Нүктенің түзу сызықты қозғалысы. Түзу сызықты қозғалыстағы нүктенің қисықтық радиусы шексіздікке тең. Мұндай қозғалыста (36) өрнегінен нормаль үдеудің нөлге айналатынын, ал толық үдеудің жанама үдеуге тең екенін көреміз:

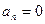, демек .

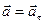Бұл жағдайда жылдамдықтың тек шамасы ғана өзгереді, демек жанама үдеу жылдамдық шамасының өзгеруін сипаттайды.

2. Бірқалыпты қозғалыс. Қозғалыс барысында жылдамдық шамасы әрқашан тұрақты болатын қозғалыс бірқалыпты қозғалыс деп аталады. Мұндай қозғалыс кезінде (35) өрнегіне сәйкес жанама үдеу нөлге тең, ал толық үдеу тек нормаль үдеуге тең болады:

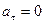, демек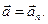

Мұндай қозғалыста жылдамдықтың тек бағыты ғана өзгереді, сондықтан нормаль үдеу жылдамдық бағытының өзгеруін сипаттайды.

3. Нүктенің бірқалыпты түзу сызықты қозғалысы. Нүкте бір мезгілде бірқалыпты және түзу сызықты қозғалыс жасағандықтан оның жанама және нормаль үдеулері бір мезгілде нөлге айналады. Демек, мұндай қозғалыста нүктенің толық үдеуі де нөлге тең болады:

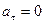және 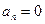, демек .

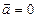Бірқалыпты және түзу сызықты қозғалыстағы нүкте жылдамдығының шамасы да, бағыты да тұрақты болады.

4. Бірқалыпты айнымалы қозғалыс. Қозғалыс барысында жанама үдеу әрқашан тұрақты болатын қозғалыс (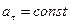) бірқалыпты айнымалы қозғалыс деп аталады.Бастапқы жылдамдықты деп алып, (35) өрнегінің екі жағын да 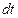-ға көбейтіп, интеграл аламыз:

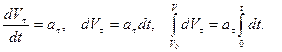
Нәтижесінде бірқалыпты айнымалы қозғалыс кезіндегі жылдамдықтың өзгеру заңын аламыз:

.

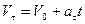Содан кейін 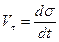екенін ескеріп, бастапқы кезде 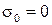деп алып, соңғы өрнекті 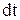-ға көбейтіп, интегралдаймыз:

.

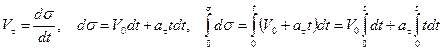Нәтижесінде нүктенің бірқалыпты айнымалы қозғалыс заңын аламыз:

.

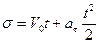Егер 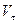мен 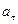таңбалары бірдей болса, нүктенің қозғалысы бірқалыпты үдемелі, ал қарсы болса – бірқалыпты кемімелі болады.

Өзіндік бақылау сұрақтары:

1. Кинематика нені зерттейді және оның негізгі мәселелері.

2. Нүкте қозғаласының берілу әдістері (векторлық, координаталық, табиғи).

3. Қозғалысы векторлық, координаталық әдістермен берілген нүктенің жылдамдығы мен үдеуін анықтау.

4. Қозғалысы табиғи әдіспен берілген нүктенің жылдамдығын анықтау.

5. Траекторияның қисықтығы мен қисықтық радиусы жайлы түсініктер.

6. Табиғи үшжақтық, оның жазықтықтары мен өстері.

7. Қозғалысы табиғи әдіспен берілген нүктенің үдеуін анықтау. Жанама және нормаль үдеулер.

8. Нүкте қозғалысының дербес жағдайлары (түзу сызықты қозғалыс, бірқалыпты қозғалыс, түзу сызықты бірқалыпты қозғалыс, бірқалыпты айнымалы қозғалыс), нүктенің үдеуі, жылдамдығы және қозғалыс заңы.

Дәріс-2. Қатты дененің қарапайым қозғалыстары.

Қатты дене кинематикасының мәселесін екіге бөлуге болады:

1) бүкіл дененің қозғалысын беру және оның кинематикалық сипаттамаларын анықтау;

2) дененің жеке нүктелерінің қозғалысының кинематикалық сипаттамаларын анықтау.

Қатты дененің екі қарапайым қозғалысын қарастырамыз. Оған дененің ілгерілемелі қозғалысы мен тұрақты өсті айналуы жатады. Осы қозғалыстардың қосындыларынан күрделі қозғалыстар алуға болады.