Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Нүктенің жылдамдығы мен үдеуі

⇐ ПредыдущаяСтр 2 из 39Следующая ⇒

Енді нүкте қозғалысы әртүрлі тәсілмен берілген кезде оның негізгі кинематикалық сипаттамаларының қалай анықталатынын қарастырайық.

Қозғалыстағы нүктенің негізгі кинематикалық сипаттамаларының біріне жылдамдық жатады. Нүктенің жылдамдығы деп оның қозғалысының жылдамдығы мен бағытын сипаттайтын векторлық шаманы айтады.

1. Векторлық тәсіл. Нүктенің 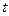уақыттағы орны 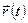радиус-вектормен, ал 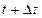уақыттағы орны 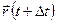радиус-вектормен анықталсын (4-сурет). Осы векторлардың айырмасын 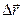арқылы белгілейік, яғни

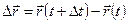. (8)

Бұл вектор нүктенің элементар 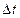уақыттағы элементар орын ауыстыруы деп аталады.

Элементар 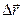орын ауыстыру векторының элементар 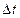уақытқа қатынасы нүктенің орташа жылдамдығы деп аталады:

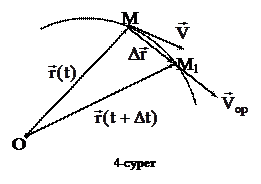
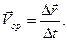(9)

Орташа жылдамдықтыңвекторы 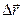векторы сияқты бағытталады.

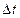нөлге ұмтылған кездегі 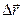мен 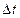қатынасының шегі нүкте жылдамдығы деп аталады:

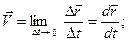(10)

демек, нүкте жылдамдығының векторы оның радиус-векторынан уақыт бойынша алынған бірінші туындыға тең екен:

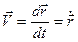. (11)

Жылдамдық векторы траекторияға жанама бойымен бағытталады (4-сурет).

Түзу сызықты қозғалыс кезінде жылдамдық векторы осы түзудің бойымен бағытталып, оның тек сандық шамасы ғана өзгере алады. Ал қисық сызықты қозғалыс кезінде жылдамдық векторының сандық шамасымен қатар бағыты да өзгеріп отырады. Жылдамдықтың өлшем бірлігі ретінде м/с немесе км/сағ. қолданылады.

Нүктенің үдеуі деп оның жылдамдығының модулі мен бағытының өзгеруін сипаттайтын векторлық шаманы айтады.

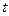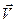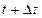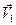Нүктенің уақыттағы орны М және жылдамдығы , ал уақыттағы орны және жылдамдығы болсын (5-сурет).

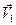векторын нүктеден М нүктеге көшіріп 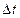уақыт аралығындағы жылдамдықтың өзгеру векторы деп аталатын вектор енгізейік:

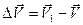. (12)

Осы вектордың өзгеріс болатын уақытқа қатынасы 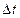уақыт аралығындағы нүктенің орташа үдеуі деп аталады:

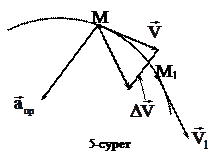
. (13)

Бұл вектор 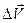векторы сияқты бағытталады.

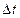нөлге ұмтылған кездегі 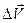мен 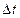қатынасының шегі нүктенің үдеуі деп аталады:

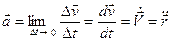. (14)

Демек, нүкте үдеуінің векторы оның жылдамдық векторынан уақыт бойынша алынған бірінші туындыға немесе радиус-векторынан уақыт бойынша алынған екінші туындыға тең екен.

Үдеудің өлшем бірлігі ретінде м/с2 қолданылады.

Нүкте үдеуінің векторы әрқашан нүкте траекториясының ойыс жағына қарай бағытталады.

2. Координаталық тәсіл. 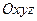декарттық координата жүйесіндегі нүкте қозғалысын қарастырайық. Сонда 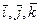бірлік вектоларының тұрақты екендігін ескеріп, (11) өрнегінен мынаны аламыз:

.

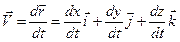Осыдан нүкте жылдамдығы векторының декарттық координата өстеріне проекцияларын аламыз:

. (15)

Нүкте жылдамдығының векторын былай жазуға болады:

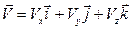. (16)

Нүкте жылдамдығының сан шамасы мына өрнекпен анықталады:

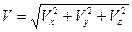, (17)

ал бағыты – бағыттаушы косинустармен анықталады:

. (18)

Енді нүкте үдеуін табу үшін (14) өрнегіне сәйкес (16) өрнегінен уақыт бойынша туынды аламыз:

.

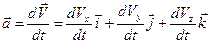Осыдан нүкте үдеуі векторының декарттық координата өстеріне проекцияларын аламыз:

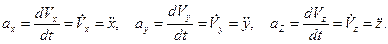(19)

Нүкте үдеуінің векторы былай жазылады:

, (20)

сонда нүкте үдеуінің сан шамасы:

. (21)

Үдеу векторының бағыттаушы косинустары:

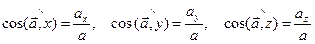. (22)

3. Табиғи тәсіл. Нүктенің 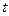уақыттағы орны 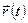радиус-вектормен, ал 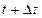уақыттағы орны 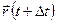радиус-вектормен анықталсын (6а-сурет).


доғасының ұзындығын 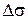деп белгілейміз. 6 а) суретте 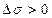, ал 6 ә) суретте – . Енді (10) өрнегін түрлендіреміз

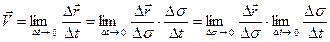, (23)

мұндағы

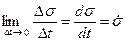. (24)

Егер 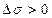болса 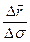векторы 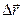векторымен бағыттас, ал болса – қарсы бағытта болады. Демек, екі жағдайда да доға санағының оң бағытына қарай бағытталады екен. Сонда сандық шамасы бірге тең 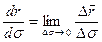векторы траекторияға жанама бойымен доға санағының оң бағытына қарай бағытталатын болады. Бұл 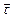векторы жанаманың бірлік векторы деп аталады:

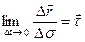. (25)

(24) және (25) өрнектерін (23) өрнегіне қойып, қозғалысы табиғи тәсілмен берілген нүкте жылдамдығы векторының өрнегін аламыз:

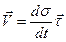. (26)

Нүкте жылдамдығы векторының жанама өске проекциясын анықтайтын белгілеу ендіруге болады (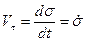), сонда жылдамдықтың векторы былай өрнектеледі:

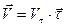. (27)

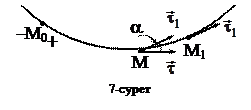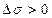Егер болса жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай (6 а) сурет), ал болса – теріс бағытына қарай бағытталады (6 ә) сурет). Жылдамдықтың сан шамасы мынау:

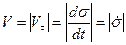. (28)

Қозғалысы табиғи тәсілмен берілген нүкте үдеуінің векторын анықтайтын өрнек алу үшін дифференциалдық геометриядан кейбір ұғымдар енгіземіз. Ол үшін траектория бойындағы жақын орналасқан екі нүктені (М және М1) қарастырайық (7-сурет), Осы нүктелерге жүргізілген жанамалардың бірлік векторларын 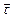және 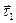арқылы белгілеп, 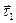векторын М1 нүктесінен М -ге көшірейік. Сонда 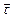мен 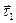бірлік векторлары арасындағы бұрышы сыбайлас бұрыш деп аталады. Егер 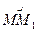доғасының ұзындығын 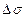деп белгілесек, доға ұзындығы нөлге ұмтылған кездегі сыбайлас бұрыштың доға ұзындығына қатынасының шегі траекторияның қисықтығы деп аталады:

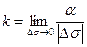. (29)

Қисықтыққа кері шама қисықтық радиусы деп аталады:

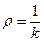. (30)

Егер нүкте түзу сызықты қозғалыста болса нүктенің қисықтығы нөлге, ал қисықтық радиусы шексіздікке тең болады. Шеңбердің қисықтығы оның барлық нүктелерінде бірдей және шеңбер радиусына кері шамаға тең, ал қисықтық радиусы шеңбер радиусына тең.

Енді М нүктесіндегі 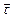және 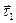векторлары арқылы жазықтық жүргізейік. Бұл жазықтық 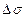нөлге ұмтылғанда жанасушы жазықтық деп аталады. 8-суретте бұл жазықтық 1 санымен белгіленген. Егер нүкте жазықтықта қозғалса, онда нүкте траекториясы толығымен жанасушы жазықтықта жатады. М нүктесі арқылы жанама өске перпендикуляр жазықтық жүргіземіз (2 жазықтық). Бұл жазықтық нормаль жазықтық деп аталады. Жанасушы жазықтық пен нормаль жазықтықтың жанасу сызығы бас нормаль деп аталады. Оның бірлік векторы 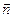траекторияның ойыс жағына қарай бағытталған. М нүктесі арқылы бас нормальға перпендикуляр жазықтық түзулеуші жазықтық деп аталады (3 жазықтық). Нормаль жазықтық пен түзулеуші жазықтықтың жанасу сызығы бинормаль деп аталады. Оның 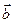бірлік векторы 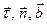векторлары оң координата жүйесін құратындай етіп бағытталады (8-сурет).


 
 

 

 


Жанасушы, нормаль және түзулеуші жазықтықтар құратын үшжақтық табиғи үшжақтық деп, ал жанама өс, бас нормаль және бинормаль – табиғи үшжақтықтың өстері деп аталады. Нүкте қозғалғанда жанама өстің, бас нормальдің және бинормальдің бірлік векторларының сан мәндері тұрақты болып қалады да, бағыттары өзгеріп отырады.

Нүктенің үдеуін анықтау үшін қозғалыс кезінде 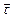векторы бағытын өзгертетінін ескере отырып (14) өрнекке сәйкес нүктенің (27) жылдамдық векторынан бірінші туынды аламыз

. (31)

Жанама өстің бірлік векторынан уақыт бойынша алынған туындыны біраз түрлендіруден кейін былай жазуға болады:

. (32)

(32)-ні (31)-ге қойып мынаны аламыз:

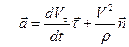. (33)

(33) өрнегінен нүкте үдеуінің векторы жанасушы жазықтықта жататынын және екі құраушыдан (жанама және нормаль) тұратынын көреміз.

Үдеудің жанама құраушысы траекторияға жанама бойымен бағытталады [егер 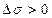болса қозғалыстың оң бағытына қарай (9 а) сурет), егер болса – теріс бағытына қарай (9 ә) сурет)] және мына өрнекпен анықталады:

.

Үдеудің нормаль құраушысы бас нормаль бойымен траекторияның ойыс жағына қарай бағытталады (9-сурет) және мына өрнекпен анықталады:

.

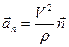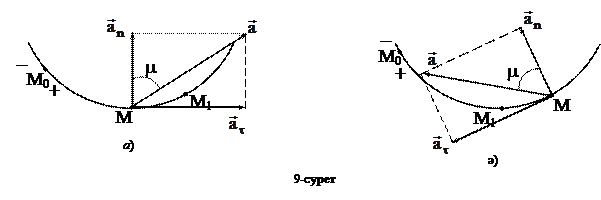Сонымен, нүктенің толық үдеуінің векторы үдеудің жанама және нормаль құраушыларының геометриялық қосындысына тең екен:


. (34)

Үдеудің жанама өске проекциясы нүктенің жанама (тангенциалдық) үдеуі деп аталады:

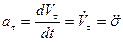, (35)

ал үдеудің бас нормальға проекциясы нүктенің нормаль үдеуі деп аталады:

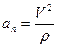, (36)

мұндағы r – траекторияның қисықтық радиусы.

Нүктенің толық үдеуінің сан шамасы (модулі):

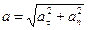. (37)

Егер нүктенің толық үдеу векторының бас нормальмен құратын бұрышын 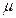деп белгілесек, онда үдеу векторының бағыты осы бұрыштың тангенсімен анықталады (9-сурет):

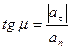. (38)

 

⇐ Предыдущая12345678910Следующая ⇒





Date: 2015-09-03; view: 3863; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.102 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию