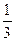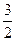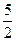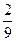Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Биномиальный закон распределения. Закон Пуассона
|
|
Если вероятность наступления случайного события в каждом испытании равна p, то вероятность того, что при n испытаниях событие A наступит k раз, находится по формуле Бернулли:
 , где
, где 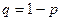 .
.
Закон распределения случайной величины X, которая может принимать n+1 значение (0, 1, …, n), описываемый формулой Бернулли, называется биномиальным.
Закон распределения случайной величины X, которая может принимать любые целые неотрицательные значения (0, 1, …, n), описываемый формулой
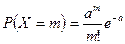 , где
, где 
носит название закона Пуассона, дающего более точное значение при малых p.
10. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений:
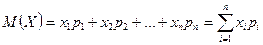
Математическое ожидание непрерывной случайной величины X определяется равенством 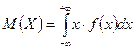 (при условии, что значение этого интеграла конечно).
(при условии, что значение этого интеграла конечно).
11. Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
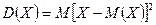 .
.
Легко получить для вычисления дисперсии более удобную формулу:

Дисперсия случайной величины есть мера рассеяния ее значений около ее математического ожидания.
Средним квадратическим отклонением случайной величины X называется величина 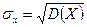 .
.
12. Свойства математического ожидания случайной величины:
1. 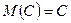 , где
, где  ;
;
2. 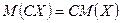 , где
, где  ;
;
3.  , где X и Y – независимые случайные величины;
, где X и Y – независимые случайные величины;
4. 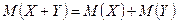 .
.
13. Свойства дисперсии случайной величины:
1. 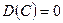 , где
, где  ;
;
2. 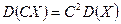 , где
, где  ;
;
3. 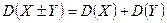 , где X и Y – независимые случайные величины.
, где X и Y – независимые случайные величины.
Пример 1. Среди 30 курсантов взвода 8 отличников. Для внеочередного дежурства назначено 5 курсантов. Найти вероятность того, что среди дежурных отличников будет нечетное число.
Решение. Введем обозначения:  ,
, 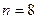 ,
, 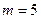 ,
, 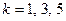 . Общее число возможных элементарных исходов испытания равно числу способов, которыми можно назначить m курсантов из N курсантов, т.е.
. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно назначить m курсантов из N курсантов, т.е. 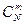 – числу сочетания из N элементов по m.
– числу сочетания из N элементов по m.
Посчитаем число исходов, благоприятствующих интересующему нас событию (среди m курсантов ровно k отличников): k отличников можно выбрать из n отличников 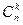 способами, при этом остальные
способами, при этом остальные 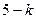 курсантов выбираются из
курсантов выбираются из 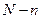 курсантов
курсантов 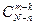 способами,
способами, 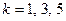 . Следовательно, число благоприятствующих исходов равно
. Следовательно, число благоприятствующих исходов равно 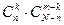 . События, состоящие в том, что число отличников среди выбранных пяти курсантов 1, 3 или 5, являются несовместными. По теореме сложения вероятностей для несовместных событий получаем:
. События, состоящие в том, что число отличников среди выбранных пяти курсантов 1, 3 или 5, являются несовместными. По теореме сложения вероятностей для несовместных событий получаем:
 ,
,
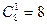 ,
, 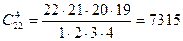 ,
, 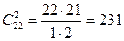 ,
,
 , т.к.
, т.к.  , то
, то 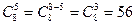 ,
,
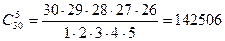 ,
, 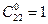 .
.
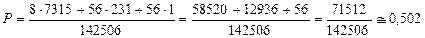 .
.
Пример 2. Для сигнализации об аварии на некотором объекте установлены сигнализаторы 5 типов: А, Б, В, Г, Д, каждый из которых сработает в случае аварии соответственно с вероятностями 0,9; 0,8; 0,7; 0,6; 0,5. Найти вероятность того, что в случае аварии сработают сигнализаторы только типов Г и Д.
Решение. Имеем пять сигнализаторов А, Б, В, Г, Д. Вероятности того, что сигнализаторы сработают в случае аварии соответственно равны p1, p2, p3, p4, p5 (p1= 0,9, p2= 0,8, p3= 0,7, p4 =0,6, p5 =0,5).
Обозначим через А1, А2, А3, А4, А5 события, состоящие в том, что сработают соответственно сигнализаторы А, Б, В, Г, Д, при этом  ,
, 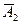 ,
, 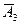 ,
,  ,
,  – противоположные им события. Вероятности противоположных событий
– противоположные им события. Вероятности противоположных событий 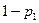 ,
, 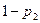 ,
, 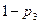 ,
, 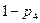 ,
,  соответственно. Требуется найти вероятность события
соответственно. Требуется найти вероятность события 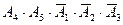 .
.
По теореме умножения вероятностей для независимых событий получаем:
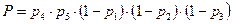 ,
,
 .
.
Пример 3. Перед возгоранием в здании могло находиться 10 человек. Все первоначальные гипотезы Нi, состоящие в том, что в здании было i человек (i =0,1,2,3,4,5,6,7,8,9,10) равновероятны. В первые же минуты после пожара был спасен один человек. Переоценить вероятность гипотезы Нi, где i = 10.
Решение. Для решения задачи используем формулу Байеса.
Пусть A – событие, состоящее в том, что спасен один человек в первые же минуты после пожара. Рассмотрим гипотезы:
H0 – в помещении не было людей,
H1 – в помещении был один человек,
H2 – в помещении было два человека,
…………………………………………
Hk – в помещении было k человек (k = 0, 1, 2,…, 10).
Так как гипотезы равновероятны, то
 .
.
Подсчитаем условные вероятности события A, соответствующие гипотезам:
 ,
, 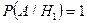 ,
,  ,…,
,…, 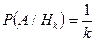 ,
,
(k = 1, 2,…, 10).
Требуется найти 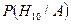 по формуле Байеса
по формуле Байеса
 ,
,
где 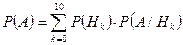 .
.
Имеем
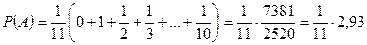 ,
,
 .
.
Пример 4. Вероятность попадания в цель при одном выстреле равна 2/3. Найти вероятность того, что при 6 выстрелах будет четное число попаданий.
Решение. Имеем 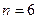 ,
, 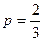 ,
, 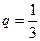 . Используем формулу Бернулли:
. Используем формулу Бернулли:
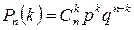 ,
,
так как независимые испытания проводятся в одинаковых условиях. Здесь k = 0, 2, 4, 6.
События, состоящие в том, что при шести выстрелах число попаданий 0, 2, 4 или 6, являются несовместными. По теореме сложения вероятностей для несовместных событий получаем:
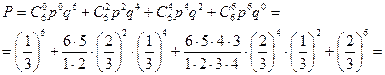
 .
.
Пример 5. Случайные величины X и Y независимо друг от друга могут с равной вероятностью принимать лишь одно из трех значений 1, 2, 3. Найти закон распределения, математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины Z и вероятность того, что случайная величина Z отклонится по абсолютной величине от своего математического ожидания не более, чем на среднее квадратическое отклонение, где  .
.
Решение. Составим ряды распределения случайных величин X, Y, Z, где 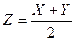 .
.
| X |
| Y |
|
| Z |
| ||||||||||||||||
| Z |
|
Подсчитаем числовые характеристики X, Y и Z.
 .
.
Математические ожидания X, Y и Z:
 ,
,
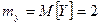 ,
, 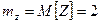 .
.
Дисперсии X, Y и Z:
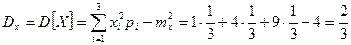 ,
,
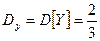 .
.
Так как X и Y независимые случайные величины, то
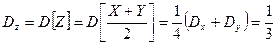 .
.
Для проверки подсчитаем Dz вторым способом:
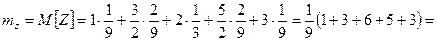
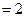 ,
,
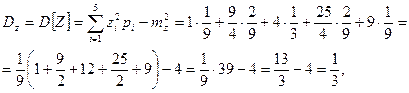
при этом среднее квадратическое отклонение 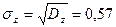 .
.
Требуется найти  .
.
Получим
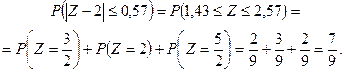
Пример 6. Для некоторого города в течении месяца (30 суток) в среднем поступает 120 сигналов о возгорании. Найти вероятность того, что в течение суток число сигналов о возгорании окажется по крайней мере один.
Решение. Имеем распределение Пуассона. Математическое ожидание a числа сигналов о возгорании в течение суток 
 .
.
Пусть m – число сигналов о возгорании в течение суток. Требуется найти 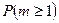 .
.
Воспользуемся формулой Пуассона:
 .
.
Получим

Пример 7. Случайная величина X принимает значения лишь в интервале (0;1) с плотностью вероятности вида  . Найти значение параметра а, математическое ожидание, дисперсию, среднее квадратическое отклонение и вероятность того, что случайная величина X не превзойдет своего среднего значения, если
. Найти значение параметра а, математическое ожидание, дисперсию, среднее квадратическое отклонение и вероятность того, что случайная величина X не превзойдет своего среднего значения, если 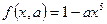 .
.
Решение. 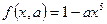 .
.
По свойству плотности 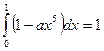 ,
,
откуда 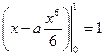 ,
, 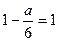 ,
,  .
.
Найдем числовые характеристики:
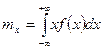 ,
,  ,
, 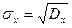 .
.
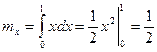 ,
,
 ,
, 
 .
.
Вероятность того, что случайная величина X не превзойдет своего среднего значения:
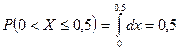 .
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Шипачев В.С. Высшая математика. - М.: Высшая школа, 2001. – 480 с.
2. Шипачев В.С. Задачник по высшей математике. - М.: Высшая школа, 2000. – 304 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Учеб. пособие для вузов. - М.: Изд. дом «ОНИКС 21 век»: Мир и Образование, 2003. - Ч. I. – 304 с.; Ч. II. – 416 c.
4. Письменный Д.Т. Конспект лекций по высшей математике. - М.: Рольф, 2001. - Ч. I. - 288 с.; Ч. II. - 256 c.
5. Вентцель Е.С. Теория вероятностей. - М.: Высшая школа, 2001. – 576 с.
6. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. - М.: Высшая школа, 2000. – 368 с.
7. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2001. – 480 с.
8. Гмурман В.Е. Руководство по решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 2001. – 400 с.
Родионов Евгений Григорьевич
Старостина Елена Вадимовна
Фомичёв Дмитрий Сергеевич
Date: 2015-08-15; view: 1406; Нарушение авторских прав