Основные теоретические сведения. 1. Определителем (детерминантом) -го порядка называется число , равное алгебраической сумме членов

1. Определителем (детерминантом) 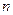-го порядка называется число , равное алгебраической сумме 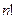членов, составленных определенным образом из элементов 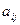определителя. Обозначение:

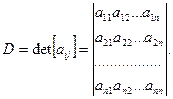
Алгебраическим дополнением элемента 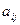определителя 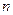-го порядка называется определитель 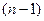-го порядка, полученный из исходного вычеркиванием 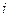-й строки и 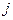-го столбца и умноженный на .

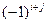Рекуррентная формула для вычисления определителя 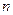-го порядка имеет вид

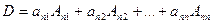
(разложение определителя по элементам 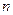-й строки).

Определитель второго порядка

.

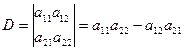2. Скалярным произведением двух векторов 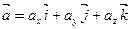и 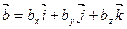называется число, определяемое равенством

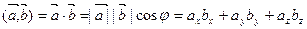, (1)

где 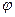- угол между векторам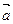и и .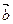

3. Векторным произведением двух векторов 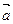и 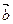называется вектор 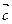, длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам 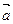и 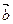так, что векторы 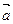, ,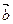, 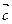образуют правую тройку (рис.1):

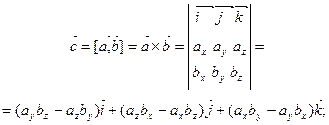(2)

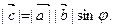
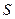Геометрически равен площади параллелограмма, построенного на векторах 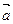и :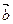

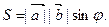
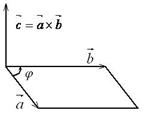
Рис.1 Рис.2

4. Смешанное произведение трех векторов , , 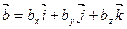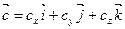есть число, равное

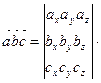(3)

Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах , , .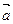

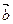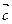5. Общее уравнение плоскости 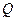имеет вид

,

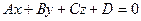где 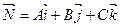- нормальный вектор плоскости (рис.2).

Уравнение плоскости, проходящей через три заданные точк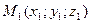и , и , имеет вид

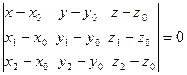. (4)

Угол между двумя плоскостями, имеющими нормальные векторы 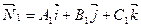и 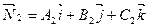, определяется как угол между 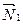и 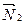; косинус этого угла находится по формуле

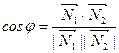. (5)

6. Уравнения прямой в пространстве, проходящей через две заданные точки и 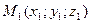, имеют вид

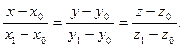(6)

7. Матрицей 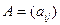размера называется прямоугольная таблица чисел, состоящая из 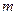строк и 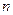столбцов:

.

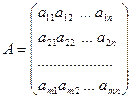Произведением матрицы 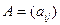размера 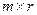на матрицу 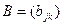размера 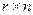называется матрица 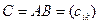размера с элементами

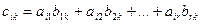(7)

(поэлементное умножение 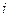-й строки матрицы на 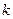-й столбец матрицы ).

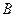Матрица размера 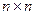называется квадратной матрицей 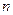-го порядка. Элементы 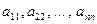образуют главную диагональ матрицы. Определитель, составленный из элементов квадратной матрицы, называется определителем матрицы и обозначается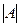 или .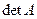

Матрица 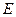с элементами 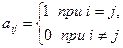называется единичной матрицей 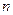-го порядка.

Матрица 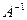называется обратной к матрице (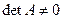), если

. (8)

Элементы 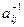обратной матрицы 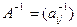вычисляются по формулам

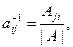(9)

где 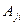- алгебраическое дополнение элемента 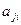матрицы , а 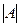- ее определитель.

8. Система трех линейных уравнений с тремя неизвестными 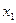, , 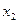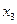имеет вид

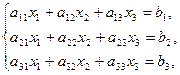(10)

где 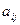- коэффициенты системы; 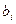- свободные члены. Определитель третьего порядка 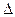, составленный из коэффициентов при неизвестных, называется определителем системы. Если 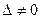, то единственное решение системы (10) выражается формулами Крамера:

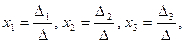(11)

где 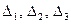- определители третьего порядка, получаемые из определителя системы 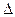заменой 1, 2 или 3-го столбца соответственно свободными членами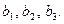

Систему (10) можно записать в матричной форме: ,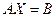

где , , .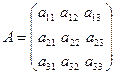

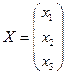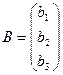Тогда ее решение имеет вид

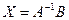, (12)

если определитель системы отличен от нуля.

9. Кривые второго порядка: кривые, описываемые уравнениями вида:

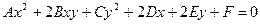. (13)

Окружностью (рис.3) называется множество всех точек плоскости, равноудаленных от данной точки, называемой центром окружности.

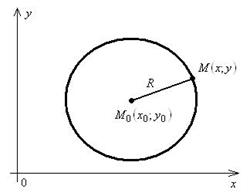
Рис.3

Каноническое уравнение окружности:

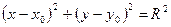, (14)

где т. 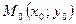– центр окружности, 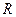– радиус окружности.

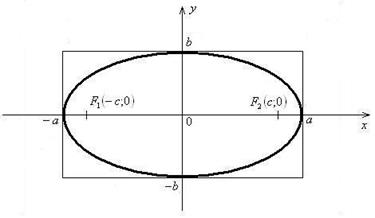
Рис.4

Эллипсом (рис.4) называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение эллипса:

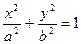. (15)

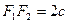– фокусное расстояние;

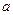– большая полуось; 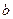– малая полуось => .

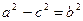Эксцентриситет эллипса: ; .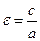

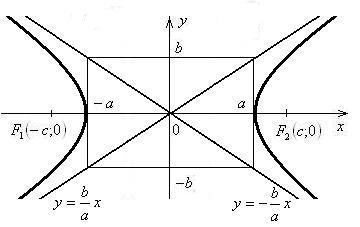
Рис.5

Гиперболой (рис.5) называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы:

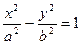. (16)

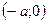и 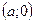– вершины гиперболы;

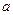– действительная полуось; 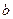– мнимая полуось => .

Асимптоты гиперболы: .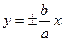

Эксцентриситет гиперболы: .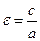

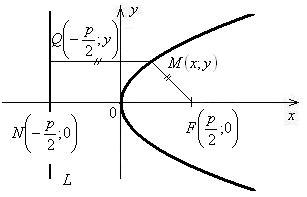
Рис.6

Параболой (рис.6) называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Расстояние от фокуса 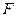до директрисы называется параметром параболы и обозначается через .

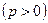Каноническое уравнение параболы:

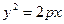. (17)

Директриса параболы: .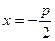

10. Выражение вида 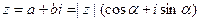называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь 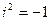, 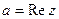- действительная часть, а 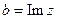- мнимая часть комплексного числа 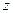; 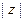и 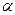- модуль и аргумент числа :

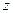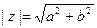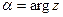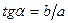, (). (18)

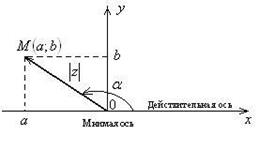
Комплексное число 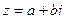изображается на координатной плоскости точкой или вектором 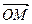, начало которого совпадает с началом координат, а конец – с точкой (рис.7).

Аргумент 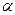комплексного числа 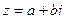можно находить так:

1) найти острый угол ;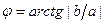

2) если 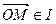четверти, то ;

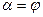если 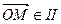четверти, то ;

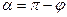если 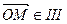четверти, то ;

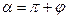если 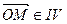четверти, то .

Рис.7

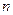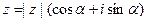Возведение в натуральную степень числа производится по формуле

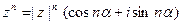, (19)

которая называется формулой Муавра.

Извлечение корня 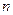-й степени ( 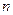- натуральное число) из числа 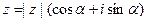(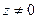) производится по формуле

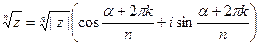, (20)

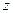где - арифметический корень из модуля , а 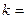0, 1,…, .

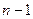Пример 1. По координатам вершин пирамиды 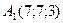, , 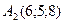, 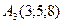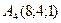найти: 1) длины ребер 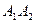и 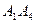; 2) угол между ребрам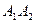и и 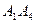; 3) площадь грани ; 4) объем пирамиды .

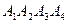Решение: 1) Находим векторы 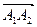и :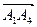

;

.

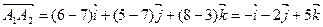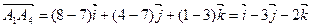Длины этих векторов, т.е. длины ребер 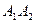и 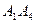, таковы:

;

.

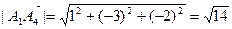2) Скалярное произведение векторов 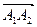и 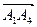находим по формуле (1):

,

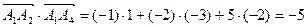а косинус угла между ними – по формуле (5):

.

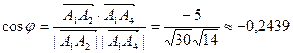Отсюда следует, что 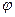- тупой угол, равный 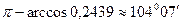. Это и есть искомый угол между ребрам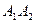и и .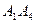

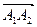3) Площадь грани равна половине площади параллелограмма, построенного на векторах и 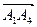, т.е. половине модуля векторного произведения этих векторов [см. формулу (2)]:

.

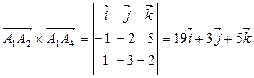Здесь определитель вычисляется с помощью разложения по первой строке. Следовательно,

.

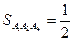
4) Объем 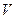пирамиды равен 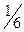объема параллелепипеда, построенного на векторах 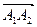, , 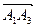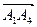. Вектор 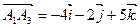Используя формулу (3), получаем

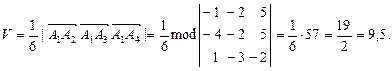
Пример 2. Найти угол между плоскостью 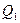, проходящей через точки 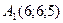, , 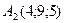, 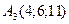и плоскостью 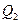, заданной уравнением .

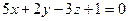Решение: Уравнение плоскости 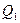находим по формуле (4):

, ,

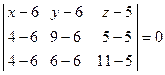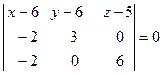т. е.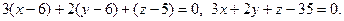

По уравнениям плоскостей определяем их нормальные векторы: 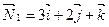, 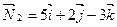. Угол 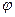между плоскостям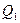и и 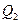находим по формуле (5):

,

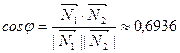откуда .

Пример 3. Составить уравнение прямой, проходящей через точки и .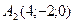

Решение: Используя формулу (6), получаем

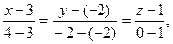
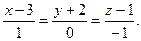
Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости

Пример 4. С помощью формул Крамера найти решение системы линейных уравнений

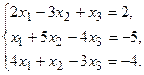(21)

Решение: Вычислим определитель системы

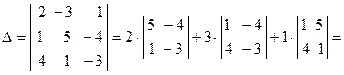
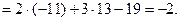
Так как 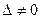, то решение системы может быть найдено по формулам Крамера (11). Для этого найдем :

, ,

.

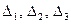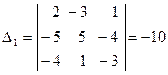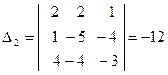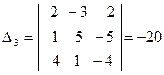Подставляя найденные значения определителей в формулы (11), получаем искомое решение системы: , , .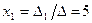

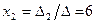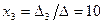Пример 5. Найти решение системы примера 4 с помощью обратной матрицы.

Решение: Здесь , , .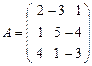

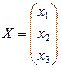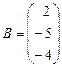Так как определитель матрицы системы отличен от нуля (см. пример 4): 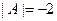, то матрица имеет обратную. Для нахождения обратной матрицы 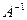вычислим алгебраические дополнения элементов матрицы :

, , ,

, , ,

, , .

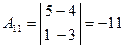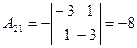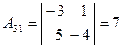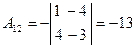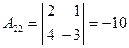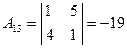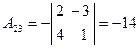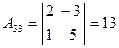Согласно формуле (9), матрица 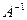, обратная к , имеет вид

.

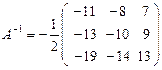Матричное решение системы (21) в силу формулы (12) имеет вид

,

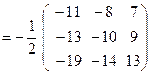
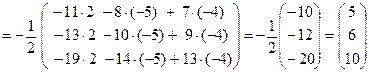откуда следует (из условия равенства двух матриц), что , , .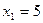

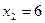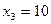Пример 6. Даны координаты вершин треугольника АВС: А(-1;2), В(5;-1), С(-4;-5). Найти: 1) уравнение медианы АЕ; 2) уравнение и длину высоты СD; 3) уравнение прямой, проходящей через точку Е параллельно стороне АВ.

Решение: 1) Для составления уравнения медианы АЕ найдем сначала координаты точки Е, которая лежит на середине отрезка ВС:

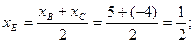
Уравнение прямой, проходящей через две заданные точки плоскости А(x₁;y₁) и В(x₂;y₂), имеет вид

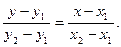(22)

Теперь, подставив в (22) координаты точек А и Е, получаем уравнение медианы:

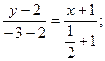
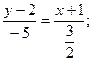
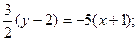
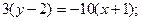
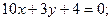(АЕ).

2) Для составления уравнения высоты СD воспользуемся уравнением прямой, проходящей через заданную точку М₀(x₀;y₀) с заданным угловым коэффициентом 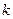, которое имеет вид

, (23)

и условием перпендикулярности прямых АВ и СD, которое выражается соотношением 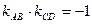, откуда . Подставив в (23) вместо 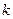значение , а вместо x₀, y₀ координаты точки С, получим уравнение высоты СD:

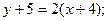
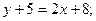
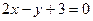(CD).

Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния 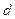от заданной точки М₀(x₀;y₀) до заданной прямой с уравнением , которая имеет вид

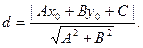(24)

Подставив в (24) вместо x₀, y₀ координаты точки С, а вместо А, В и С коэффициенты уравнения прямой АВ, получаем

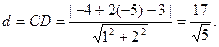
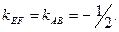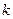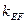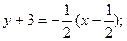
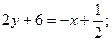
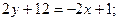
3) Так как искомая прямая ЕF параллельна прямой АВ, то Подставив в уравнение (23) вместо x₀, y₀ координаты точки Е, а вместо значение , получаем уравнение прямой 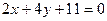ЕF:

(ЕF).

Пример 7. Составить уравнение гиперболы, проходящей через точку 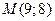, если асимптоты гиперболы имеют уравнения .

Решение:

Уравнение асимптот: => => .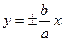

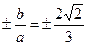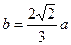Подставим данные в уравнение гиперболы (16):

=> => => => => => .

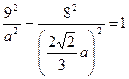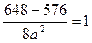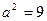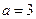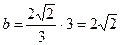Уравнение гиперболы: .

Пример 8. Записать число 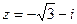в тригонометрической форме.

Решение: Находим модуль

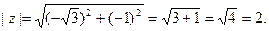
Находим угол

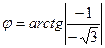
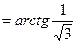
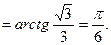
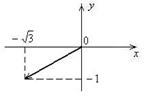
Рис.8

Вектор, соответствующий данному комплексному числу, лежит в III координатной четверти (рис.8), поэтому одним из аргументов является 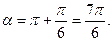Следовательно,

Это и есть тригонометрическая форма комплексного числа .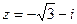

Пример 9. Записать число 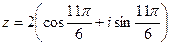в алгебраической форме.

Решение: Сначала найдем 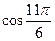и :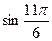

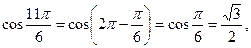
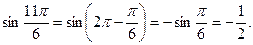
Тогда 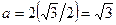, 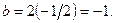Следовательно,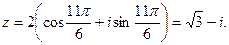

Пример 10. Вычислить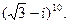

Решение: Запишем сначала число 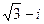в тригонометрической форме: 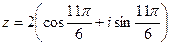(см. пример 9). Теперь воспользуемся формулой Муавра (19). Тогда

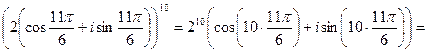
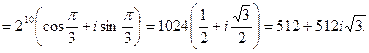
КОНТРОЛЬНАЯ РАБОТА №2

Date: 2015-08-15; view: 490; Нарушение авторских прав