Основные теоретические сведения

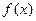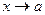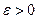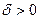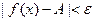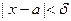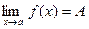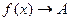1. Определение конечного предела функции в точке: число называется пределом функции при , если для любого найдется такое, что при . Обозначение: или при .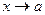

Функция 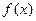() называется бесконечно малой (бесконечно большой) при 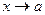, если ().

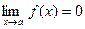Две функци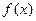и и 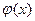, одновременно стремящиеся к нулю или бесконечности при 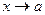, называются эквивалентными, если 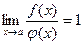. Обозначение: .

Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией, т.е.

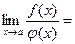
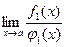, (1)

если , .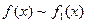

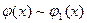2. К основным элементарным функциям относятся: 1) степенная функция 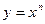; 2) показательная функция 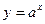; 3) логарифмическая функция 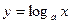; 4) тригонометрические функции: ,

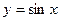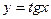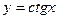, , ; 5) обратные тригонометрические функции: , , , .

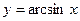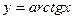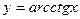Предел элементарной функции в точке области ее определения равен частному значению функции в этой точке: .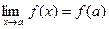

Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида

, , , , , , .

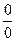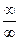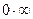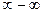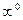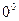Элементарными приемами раскрытия неопределенностей являются:

1) сокращение на множитель, создающий неопределенность;

2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при );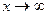

3) применение эквивалентных бесконечно малых и бесконечно больших;

4) использование первого замечательного предела:

; (2)

5) использование второго замечательного предела:

. (3)

Отметим также, что

, если ;

, если ;

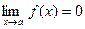, если , ;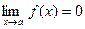

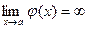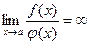, если , .

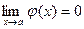3. Функция 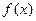называется непрерывной в точке 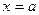, если:

1) частное значение функции в точке 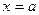равно ;

2) существуют конечные односторонние пределы функции

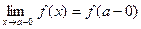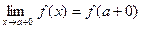, ; (4)

3) односторонние пределы равны:

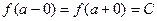; (5)

4) предельное значение функции в точке 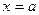равно ее частному значению :

. (6)

Обозначение: .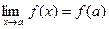

Точка 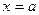называется точкой устранимого разрыва, если [нарушается условие (6)].

Точка 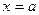называется точкой разрыва первого рода, если оба односторонних предела конечны, но 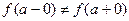[нарушается условие (5)].

Точка 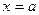называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен бесконечности или не существует [нарушается условие (4)].

4. Производной функции 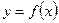в точке 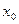называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

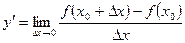(7)

или

. (8)

Функция 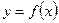, имеющая производную в каждой точке интервала , называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Обозначение: , .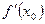

5. Физический смысл производной: Если функция 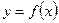описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

6. Геометрический смысл производной: Производная 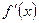в точке x равна угловому коэффициенту касательной к графику функции 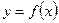в точке, абсцисса которой равна x.

7. Уравнение касательной в точке :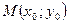

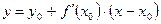. (9)

8. Уравнение нормали в точке :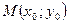

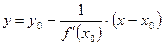, если . (10)

9. Теорема о непрерывности: Если функция дифференцируема в некоторой точке, то она непрерывна в ней.

10. Правила дифференцирования:

1. 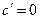, где .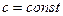

2. .

3. .

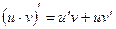4. 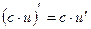, где .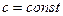

5. , .

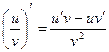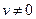11. Производная сложной и обратной функции:

Пусть 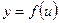и , тогда 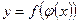– сложная функция с промежуточным аргументом 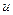и независимым аргументом x.

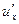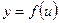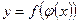Теорема: Если функция имеет производную в точке x, а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке x, которая находится по формуле .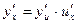

Таким образом, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Пусть 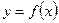и 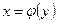– взаимно обратные функции.

Теорема: Если функция 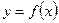строго монотонна на интервале и имеет неравную нулю производную 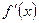в произвольной точке этого интервала, то обратная ей функция 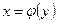также имеет производную 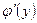в соответствующей точке, определяемую равенством 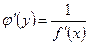или .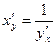

Таким образом, производная обратной функции равна обратной величине производной данной функции: .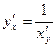

12. Производные основных элементарных функций:

1. Степенная функция : .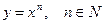

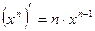2. Показательная функция: : .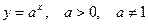

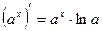3. Логарифмическая функция: 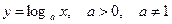: 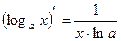. В частности, .

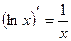4. Тригонометрические функции: ; ; ; .

; ;

; .

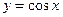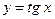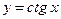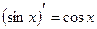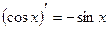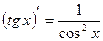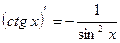5. Обратные тригонометрические функции: ; ; ; .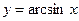

; ;

; .

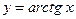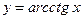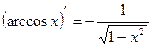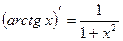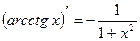13. Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность 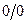или 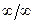) равен пределу отношения их производных:

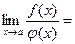
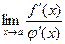, (11)

если предел справа существует.

Пример 1. Найти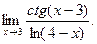

Решение: Подставляя вместо 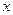его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе – бесконечно малую функцию:

Поэтому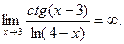

Пример 2. Найти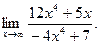

Решение: Подстановка предельного значения аргумента приводит к неопределённости вида 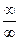. Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на 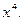В результате получим

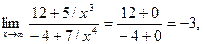
поскольку при 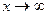функци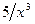и и 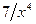являются бесконечно малыми.

Пример 3. Найти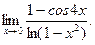

Решение: Для раскрытия получающейся здесь неопределенности вида 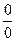используем метод замены бесконечно малых эквивалентными. Так

как при 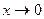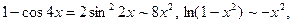то на основании формулы (1) находим

.

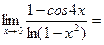
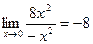Пример 4. Найти

Решение: Подстановка 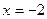приводит к неопределенности . Произведем замену переменных: 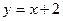, 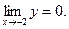Тогда

Здесь использован второй замечательный предел (3).

Пример 5. Исследовать функцию

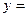
на непрерывность; найти точки разрыва функции и определить их тип. Построить схематический график функции.

Решение: Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции, т. е. точк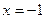и и 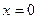. Вычислим односторонние пределы в этих точках.

Для точки 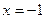имеем:

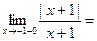
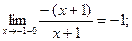
Односторонние пределы функции в точке 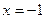существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.

Для точки 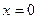получаем

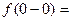
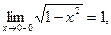
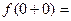
Односторонние пределы функции при 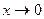равны между собой и равны частному значению функции: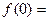 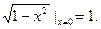Следовательно, исследуемая точка является точкой непрерывности. График данной функции приведен на рис.9.

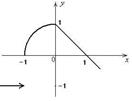
Рис.9

Пример 6. Используя правило Лопиталя, вычислить предел функций:

1) 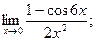2)

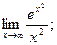
Решение: 1) Подстановка предельного значения аргумента 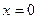приводит к неопределенности вида 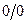. Раскроем ее с помощью правила Лопиталя (11):

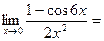
Однократное применение правила Лопиталя не приводит к раскрытию неопределенности (по-прежнему получаем 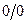), поэтому применим его еще раз:

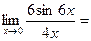
Таким образом, в результате двукратного применения правила Лопиталя находим, что искомый предел равен 9.

2) Убедившись, что имеет место неопределенность вида 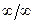, применим правило Лопиталя:

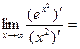
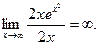
Пример 7. Найти первую производную функции 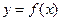, заданной параметрически:

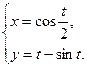
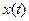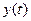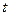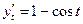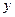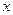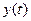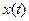Решение: Дифференцируем и по параметру : , . Искомая производная от по равна отношению производных от и от по :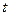

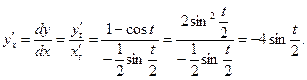
КОНТРОЛЬНАЯ РАБОТА №3

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ

ПРОИЗВОДНЫХ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Date: 2015-08-15; view: 492; Нарушение авторских прав