Основные теоретические сведения. 1. Двойной интеграл можно вычислить двумя способами:

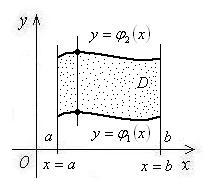
1. Двойной интеграл можно вычислить двумя способами:

; (1)

(2)

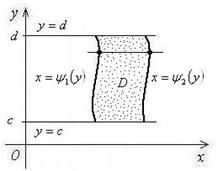
Рис.12 Рис.13

В первом случае (рис.12) область D лежит между вертикальными прямым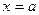и и 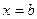, а снизу и сверху ограничена линиям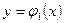и и .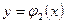

Во втором случае (рис.13) надо провести горизонтальные прямые 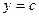и , между которыми лежит область D, а 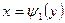и

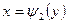- уравнения линий, ограничивающих область D слева и справа.

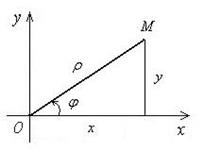
2. При переходе к полярным координатам (рис.14) надо декартовые координаты x, y выразить через полярные по формулам 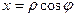, 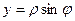и элемент площади 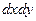заменить на .

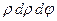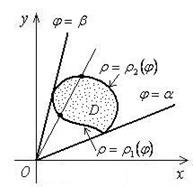
Рис.14 Рис.15

Пусть область D лежит между двумя лучами 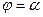, 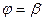и изнутри угла и снаружи ограничена линям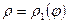и и 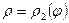(рис.15).

Тогда:

=

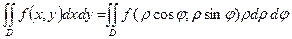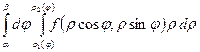= (3)

3. Криволинейные интегралы 1 рода. Если кривая 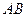задана параметрическими уравнениями 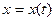, 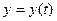(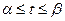), то

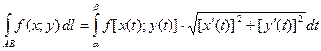(4)

Если кривая 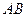задана уравнением 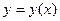, , 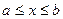то

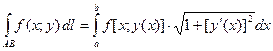(5)

4. Криволинейные интегралы 2 рода. Если кривая 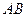задана параметрическими уравнениями 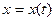, 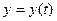(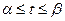), то

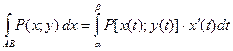
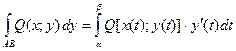
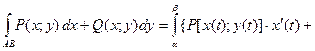
(6)

Если кривая 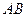задана уравнением 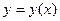, , 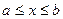то

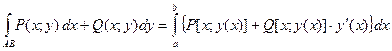(7)

5. Частной производной первого порядка функции двух переменных 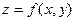по аргументу 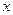называется предел

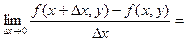
(8)

(приращение получает только один аргумент 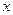). Обозначение: 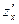, . Отыскание частной производной сводится к дифференцированию функции одной переменной 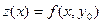, полученной при фиксировании аргумента : .

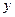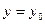Частной производной первого порядка функции двух переменных 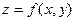по аргументу 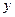называется предел

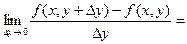
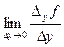(9)

(приращение получает только один аргумент 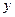). Обозначение: 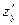, 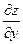. Отыскание частной производной 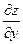сводится к дифференцированию функции одной переменной 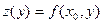, полученной при фиксировании аргумента : .

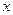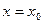6. Производная в данном направлении. Градиент функции.

Если направление l в плоскости 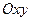характеризуется направляющими косинусами 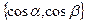и функция 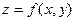дифференцируема, то производная по направлению l вычисляется по формуле

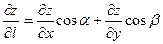. (10)

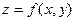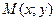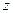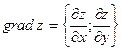Градиентом функции в точке называется вектор с началом в точке , имеющий своими координатами частные производные функции :

или 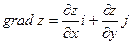. (11)

Градиент указывает направление наибыстрейшего роста функции в данной точке. Производная 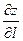в направлении градиента имеет наибольшее значение, равное

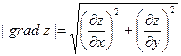. (12)

7. Экстремум функции двух переменных:

Пусть функция 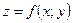определена в некоторой области , точка .

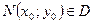Точка 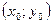называется точкой максимума функции 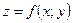, если существует такая δ-окрестность точки 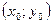, что для каждой точки 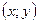, отличной от 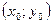, из этой окрестности выполняется неравенство .

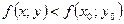Аналогично определяется точка минимума функции.

Необходимые условия экстремума: Если в точке 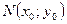дифференцируемая функция 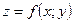имеет экстремум, то ее частные производные в этой точке равны нулю: , .

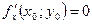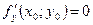Достаточное условие экстремума: Пусть в стационарной точке 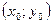и некоторой ее окрестности функция 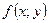имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 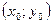значения , , 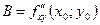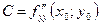. Обозначим .

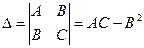Тогда:

1. Если 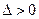, то функция 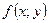в точке 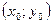имеет экстремум: максимум, если 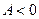; минимум, если ;

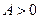2. Если 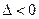, то функция 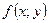в точке 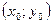экстремума не имеет.

В случае 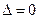экстремум в точке 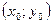может быть, может не быть. Необходимы дополнительные исследования.

Пример 1. Вычислить 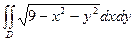, где область D – круг .

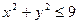Решение. Применив формулу (3), перейдем к полярным координатам:

.

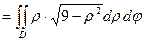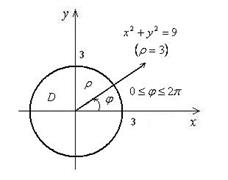Область D в полярной системе координат определяется неравенствами (см. рис.16) 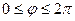, 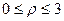. Поэтому, согласно формуле (3), имеем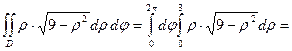

Рис.16.

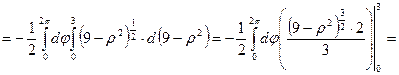
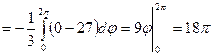
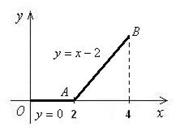
Пример 2. Вычислить 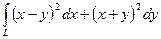, L – ломаная OAB, где , , .

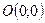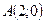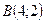Решение.

Так как 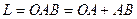(см. рис.17), то .

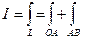Уравнение отрезка OA есть 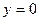, ; уравнение отрезка AB: 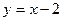, 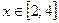. Согласно формуле (7), имеем:

Рис.17

.

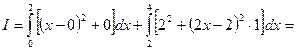
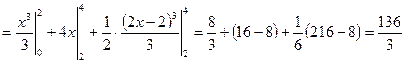Пример 3. Составить уравнение касательной и нормали к кривой 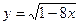в точке, абсцисса которой .

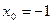Решение: Найдем ординату точки касания: 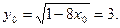Угловой коэффициент касательной равен значению производной в точке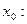

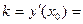
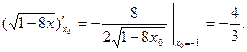
Подставляя значения 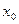, 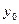и 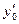в уравнения касательной 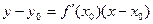и нормали 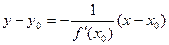, получаем:

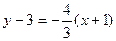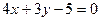, (касательная);

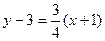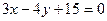, (нормаль).

Пример 4. Найти частные производные и 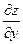функции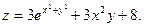

Решение: Считая функцию 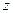функцией только одной переменной 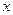, а переменную 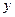рассматривая как постоянную [см. формулу (8)], находим

.

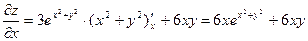Аналогично, считая 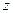функцией только 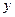, получаем

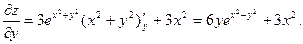
Пример 5. Дана функция 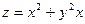. Найти: 1) градиент функции в точке 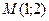; 2) производную функции в точке 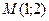по направлению вектора 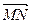, где .

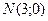Решение: 1) Найдем частные производные функции: ; 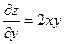и их значения в точке :

, .

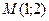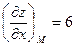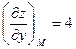По формуле (11) получим

.

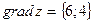2) Найдем вектор 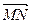и его направляющие косинусы:

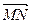= l = ;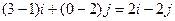

;

.

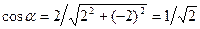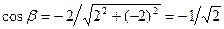По формуле (10) получим

.

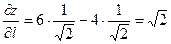Пример 6. Найти экстремум функций: .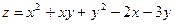

Решение:

Находим стационарные точки (необходимое условие экстремума):

;

~ ~ .

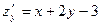
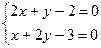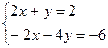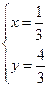Стационарная точка: .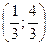

Применим достаточное условие экстремума:

; ; .

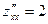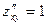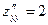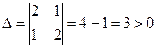– экстремум есть.

Т.к. 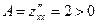– это локальный минимум.

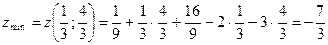– минимум.

КОНТРОЛЬНАЯ РАБОТА №5

Date: 2015-08-15; view: 443; Нарушение авторских прав