
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формулировка первого закона Ньютона
|
|
Всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. (В этой формулировке Ньютон привел закон, установленный еще Галилеем).
Эта формулировка тем самым утверждает существование инерциальных систем отсчета.
Масса и импульс тела. Сила.
Масса тела, 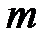
|
Физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.
Можно считать доказанным, что инертная и гравитационная массы равны друг другу(с точностью, не меньшей 10-12 их значения)
Масса – величина аддитивная (масса составного тела равна сумме масс его частей); если движение происходит со скоростями много меньше скорости света, то массу можно считать величиной постоянной, не изменяющейся при движении тела.
Единица измерения массы
 = к г. = к г.
| |
Импульс материальной точки (тела)
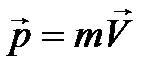
|
Векторная величина, численно равная произведению массы материальной точки(тела) на ее скорость и имеющая направление скорости
Единица измерения импульса 
| |
Сила, 
| Векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением,направлением в пространстве и точкой приложения. | |
| ОСНОВНОЙ ЗАКОН ДИНАМИКИ Общая формулировка второго закона Ньютона | ||

| Скорость изменения импульса материальной точки(тела) равна действующей на нее(него) силе. Записанное уравнение называют еще уравнением движения материальной точки | |
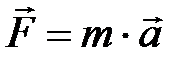 или
или
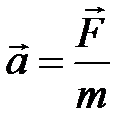
| Еще одна формулировка второго закона Ньютона
Ускорение, приобретаемое материальной точкой(телом), пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки(тела)
Единица измерения силы 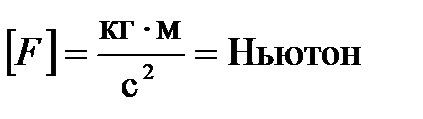 . .
| |
| Второй закон Ньютона справедлив только в инерциальных системах отсчета. | ||
| ТРЕТИЙ ЗАКОН НЬЮТОНА Формулировка третьего закона Ньютона | ||
Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия: силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

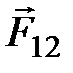 - сила, действующая на первую материальную точке со стороны второй - сила, действующая на первую материальную точке со стороны второй
 - сила, действующая на вторую материальную точку со стороны первой - сила, действующая на вторую материальную точку со стороны первой
| ||
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
В случае замкнутой системы, когда внешние силы отсутствуют (или геометрическая сумма внешних сил равна нулю) или общей формулировки второго закона Ньютона имеем 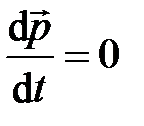 или
или 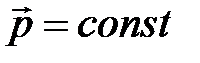 .
.
Импульс замкнутой системы сохраняется, то есть
не изменяется с течением времени.
Этот закон – фундаментальный закон природы (Он универсален).
МЕХАНИКА ТВЕРДОГО ТЕЛА
Момент инерции, 
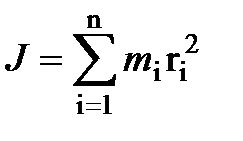
 Единицы измерения
Единицы измерения 
|
Физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси.
Суммирование производится по всем элементарным массам 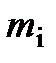 , на которые можно разбить тело.
Момент инерции – величина аддитивная: момент инерции тела равен сумме моментов инерции его частей
Момент инерции материальной точки рассчитывается как , на которые можно разбить тело.
Момент инерции – величина аддитивная: момент инерции тела равен сумме моментов инерции его частей
Момент инерции материальной точки рассчитывается как
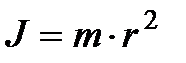 В случае непрерывного распределения масс момент инерции рассчитывается как интеграл по объему.
Здесь
В случае непрерывного распределения масс момент инерции рассчитывается как интеграл по объему.
Здесь 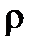 - плотность тела в данной точке; - плотность тела в данной точке;  - масса малого элемента тела объемом - масса малого элемента тела объемом 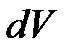 , отстоящего относительно оси вращения на расстоянии , отстоящего относительно оси вращения на расстоянии  . .

|
| МОМЕНТЫ ИНЕРЦИИ ОДНОРОДНЫХ ТЕЛ |

| МОМЕНТ СИЛЫ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА |

|
Момент силы относительно неподвижной точки О

|
Физическая величина, определяемая векторным произведением радиуса-вектора  , проведенного из точки О в точку А приложения силы, на силу , проведенного из точки О в точку А приложения силы, на силу  . .
 - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от  к к 
| ||||
Модуль вектора момента силы
Единицы измерения 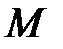
|


| ||||
| Уравнение динамики вращательного движения твердого тела | |||||
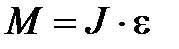
|
Момент сил твердого тела относительно оси равен произведению момента инерции относительно той же оси на угловое ускорение.
Выведем эту формулу
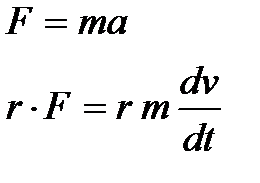 ,
но для вращательного движения ,
но для вращательного движения  тогда
тогда 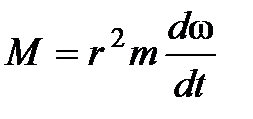 или или  Вывод сделан для материальной точки и для случая, когда угол
Вывод сделан для материальной точки и для случая, когда угол 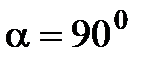 (см. выражение для модуля момента силы) (см. выражение для модуля момента силы)
| ||||
| Момент импульса |
Момент импульса материальной точки относительно неподвижной точки О

|
Физическая величина, определяемая векторным произведением радиуса-вектора  материальной точки, проведенного из точки О, на импульс материальной точки, проведенного из точки О, на импульс  этой материальной точки. этой материальной точки.
 псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от  к к 
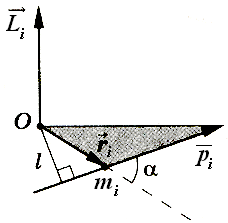
| |
| Модуль вектора момента импульса |

| |
| Момент импульса абсолютно твердого тела относительно неподвижной оси z | ||
 Единицы измерения
Единицы измерения 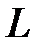

| ||
Еще одна форма записи
уравнения динамики вращательного движения твердого тела

| ||
Закон сохранения момента импульса – фундаментальный закон природы
В замкнутой системе момент внешних сил  и и  ,
тогда ,
тогда 
|
Аналогия в описании
поступательного и вращательного движений

РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ


КИНЕТИЧЕСКАЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Кинетическая энергия тела массой m , движущегося со скоростью v
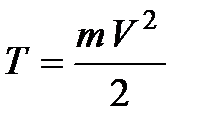 Определяется работой, которую надо совершить, чтобы сообщить телу данную скорость.
Определяется работой, которую надо совершить, чтобы сообщить телу данную скорость.
Кинетическая энергия всегда положительна; является функцией состояния системы.
Работа сил при перемещении из точки 1 в точку 2.
 .
.
Потенциальная энергия и консервативные силы
Потенциальная энергия.
Механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Потенциальное поле.
Поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений.
Консервативные силы
Сила, работа которой при перемещении тела из одного положения в другое не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений тела. Пример – сила тяжести.
Если работа консервативных сил совершается по замкнутому пути, то она равна нулю.
Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком «минус», так как работа совершается за счет убыли потенциальной энергии
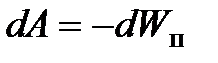 .
.
Связь между консервативной силой и потенциальной энергией.
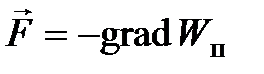 .
.
Конкретный вид функции  зависит от характера силового поля.
зависит от характера силового поля.
Потенциальная энергия тела массой 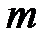 на высоте
на высоте 
 - Это выражение вытекает из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты
- Это выражение вытекает из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты  на поверхность Земли. Высота
на поверхность Земли. Высота  отсчитывается от нулевого уровня, для которого
отсчитывается от нулевого уровня, для которого 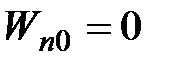 ,
, 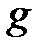 - ускорение свободного падения.
- ускорение свободного падения.
Поскольку начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!).
Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина  ),
), 
Потенциальная энергия упруго деформированного тела (пружины)
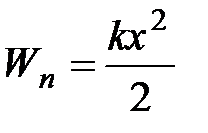 Это выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины.
Это выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины.
 - коэффициент упругости (для пружины – жесткость).
- коэффициент упругости (для пружины – жесткость).
Полная механическая энергия системы равна сумме кинетической и потенциальной энергий.

Закон сохранения и превращения энергии.
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
В этом заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.
Этот закон – фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Работа при вращении тела

Кинетическая энергия вращающегося тела

ВОПРОСЫ К СЕМИНАРУ ПО МЕХАНИКЕ
1. Как рассчитать путь S при равномерном, равнопеременном движении?
2. Как рассчитать мгновенную линейную скорость? Единицы измерения мгновенной линейной скорости?
3. Как рассчитать мгновенное линейное ускорение? Единицы измерения линейного ускорения?
4. Как рассчитать нормальное ускорение an при движении тела по криволинейной траектории? Что показывает нормальное ускорение?
5. Как рассчитать тангенциальное ускорение? Что показывает тангенциальное ускорение?
6. Как рассчитать полное ускорение?
7. Как рассчитать путь при равномерном, равнопеременном вращении с угловой скоростью w?
8. Записать формулы связи между линейными и угловыми величинами.
9. Основной закон динамики вращательного движения. Двеформулы. (В векторной форме)
10. Закон сохранения момента количества движения. Формулировка и математическая запись.
11. Как рассчитать момент силы М? (По определению). Формулу записать в векторной и скалярной формах. Единицы измерения момента силы.
12. Как рассчитать момент количества движения? (По определению). Формулу записать в векторной и скалярной формах. Единицы измерения момента количества движения.
13. Как рассчитать момент инерции J материальной точки массой m относительно оси, находящейся от нее на расстоянии r?.Единицы измерения момента инерции
14. Как рассчитать кинетическую энергию тела, движущегося поступательно? Единицы измерения энергии
15. Как рассчитать потенциальную энергию, которой обладает тело, поднятое над землей на высоту h?
16. Как рассчитать потенциальную энергию сжатой пружины, коэффициент упругости которой k?
17. Как рассчитать работу А по перемещению силой F какого-либо груза на расстояние s? Единицы измерения работы?
18. Как рассчитать мощность? Единицы измерения мощности.
19. Как рассчитать кинетическую энергию вращающегося тела?
20. Что обозначено каждой буквой в предложенной Вами формуле для расчета кинетической энергии вращающегося тела?
Date: 2015-08-15; view: 1963; Нарушение авторских прав