
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практическое задание №3. Программирование систем поддержки принятия решений в условиях неопределенности
|
|
Неопределенность является характеристикой внешней среды
(природы), в которой принимается управленческое решение о раз
витии (или функционировании) экономического объекта. Здесь будем рассматривать неопределенность «природы», вызванную отсутствием, недостатком информации о действительных условиях (факторах), при которых развивается объект управления. Внешняя среда («природа») может находиться в одном из множества возможных
состояний. Это множество может быть конечным и бесконечным.
Будем считать, что множество состояний конечно или по крайней
мере количество состояний можно пронумеровать.
Пусть Sj— состояние «природы», при этом i=1,n, где п — число возможных состояний. Все возможные состояния известны, не известно только, какое состояние будет иметь место в условиях, когда планируется реализация принимаемого управленческого решения. Будем считать, что множество управленческих решений (планов) R j также конечно и равно т. Реализация r j плана в условиях, когда «природа» находится в Sj состоянии, приводит к определенному результату, который можно оценить, введя количественную меру, В качестве этой меры могут служить выигрыши от принимаемого решения (плана); потери от принимаемого решения, а также полезность, риск и другие количественные критерии.
Данные, необходимые для принятия решения в условиях неопределенности, обычно задаются в форме матрицы, строки которой соответствуют возможным действиям (управленческим решения) Rj, а столбцы — возможным состояниям «природы» Si.
Допустим, каждому Rj-му действию и каждому возможному Si-му состоянию «природы» соответствует результат (исход), определяющий результат (выигрыш, полезность) при выборе j-го действия и реализации i-го состояния, — Vji.
 (22)
(22)
Рисунок 3-матрица для принятия решения в условиях неопределенности
Следовательно, математическая модель задачи принятия решений определяется множеством состояний {Si}, множеством планов (стратегий) {Rj} и матрицей возможных результатов || Vji||. В качестве результатов в отдельных задачах рассматривается матрица рисков || rji||.
Риск — мера несоответствия между разными возможными результатами принятия определенных стратегий (действий).
Элементы матрицы рисков ||rji|| связаны с элементами матрицы полезностей (выигрышей) следующим соотношением:

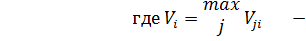
максимальный элемент в столбце i матрицы полезностей
Если матрица возможных результатов ||Vji|| представляет собой матрицу потерь (затрат), то элементы матрицы рисков ||rji|| следует определять по формуле
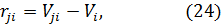
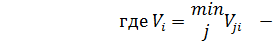
минимальный элемент в столбце i матрицы потерь (результатов).
Таким образом, риск — это разность между результатом, который можно получить, если знать действительное состояние «природы», и результатом, который будет получен при j-й стратегии.
Матрица рисков дает более наглядную картину неопределенной ситуации, чем матрица выигрышей (полезностей).
Непосредственный анализ матриц выигрышей ||Vji|| или рисков ||rji|| не позволяет в общем случае принять решение по выбору оптимальной стратегии (плана), за исключением тривиального случая, когда выигрыши при одной стратегии выше, чем при любой другой для каждого состояния «природы» (элементы матрицы выигрышей в некоторой строке больше, чем в любой из других). Другими словами, имеется в наличии «доминирующая» стратегия.
Для принятия решения в условиях неопределенности используется ряд критериев. Рассмотрим некоторые из них. Это критерий Лапласа, критерий Вальда, критерий Сэвиджа, критерий Гурвица.
1. Критерий Лапласа.
Этот критерий опирается на «принцип недостаточного основания» Лапласа, согласно которому все состояния «природы» Si, i = 1,n полагаются равновероятными. В соответствии с этим принципом каждому состоянию Si, ставится вероятность qi определяемая по формуле

При этом исходной может рассматриваться задача принятия решения в условиях риска, когда выбирается действие Rj, дающее наибольший ожидаемый выигрыш. Для принятия решения для каждого действия Rj вычисляют среднее арифметическое значение выигрыша:
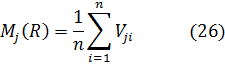
Среди Mj(R) выбирают максимальное значение, которое будет соответствовать оптимальной стратегии Rj.
Другими словами, находится действие Rj, соответствующее

Если в исходной задаче матрица возможных результатов представлена матрицей рисков ||rji||, то критерий Лапласа принимает следующий вид:
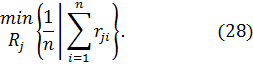
Пример 4. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Ниже приводится таблица, определяющая возможные прогнозируемые затраты на развитие провозных возможностей:
Таблица 10- прогнозируемые затраты на развитие провозных возможностей
| Варианты провозных возможностей транспортного предприятия | Варианты спроса на транспортные услуги | |||
Необходимо выбрать оптимальную стратегию.
Решение:
Согласно условию задачи, имеются четыре варианта спроса на транспортные услуги, что равнозначно наличию четырех состояний «природы»: S1, S2, S3, S4. Известны также четыре стратегии развития провозных возможностей транспортного предприятия: R1, R2, R3, R4 Затраты на развитие провозных возможностей при каждой паре Si и Rj заданы следующей матрицей (таблицей):
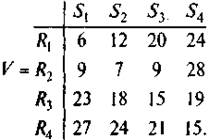
Рисунок 4-матрица для принятия решения
Принцип Лапласа предполагает, что S1, S2, S3, S4 равновероятны. Следовательно, P{S = Si }= 1/n= 1/4 = 0,25, i = 1, 2, 3, 4 и ожидаемые затраты при различных действиях R1, R2, R3, R4 составляют:

Таким образом, наилучшей стратегией развития провозных возможностей в соответствии с критерием Лапласа будет R2.
2. Критерий Вальда (минимаксный или максиминный критерий).
Применение данного критерия не требует знания вероятностей состояний Si. Этот критерий опирается на принцип наибольшей осторожности, поскольку он основывается на выборе наилучшей из наихудших стратегий Rj.
Если в исходной матрице (по условию задачи) результат Vij представляет потери лица, принимающего решение, то при выборе оптимальной стратегии используется минимаксный критерий. Для определения оптимальной стратегии Rj необходимо в каждой строке матрицы результатов найти наибольший элемент max{Vij}, а затем выбирается действие Rj (строка j), которому будет соответствовать наименьший элемент из этих наибольших элементов, т. е. действие, определяющее результат, равный
 . (29)
. (29)
j i
Если в исходной матрице по условию задачи результат Vij представляет выигрыш (полезность) лица, принимающего решение, то при выборе оптимальной стратегии используется максиминный критерий.
Для определения оптимальной стратегии Rj в каждой строке матрицы результатов находят наименьший элемент min {Vij}, а затем выбирается действие Rj (строка j), которому будут соответствовать наибольшие элементы из этих наименьших элементов, т. е. действие, определяющее результат, равный
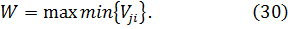
j i
Пример 5. Рассмотрим пример 4. Так как Vij в этом примере представляет потери (затраты), применим минимаксный критерий. Необходимые результаты вычисления приведены в следующей таблице:
Таблица 11-
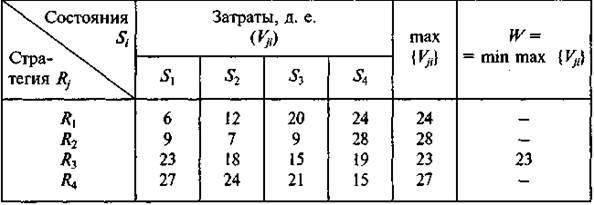
Таким образом, наилучшей стратегией развития провозных возможностей в соответствии с минимаксным критерием «лучшим из худших» будет третья, т. е. R3.
Минимаксный критерий Вальда иногда приводит к нелогичным выводам из-за своей чрезмерной «пессимистичности». «Пессимистичность» этого критерия исправляет критерий Сэвиджа.
3.Критерий Сэвиджа.
Критерий Сэвиджа использует матрицу рисков || rij ||. Элементы данной матрицы можно определить по формулам (23), (24), которые перепишем в следующем виде:
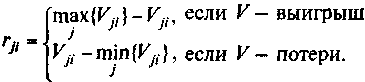 (31)
(31)
Это означает, что rij есть разность между наилучшим значением в столбце i и значениями Vji при том же i. Независимо от того, является ли Vji доходом (выигрышем) или потерями (затратами), rji в обоих случаях определяет величину потерь лица, принимающего решение. Следовательно, можно применять к rji только минимаксный критерий. Критерий Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию Rj, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск максимален).
Пример 6. Рассмотрим пример 4. Заданная матрица определяет потери (затраты). По формуле (31) вычислим элементы матрицы рисков || rij ||:
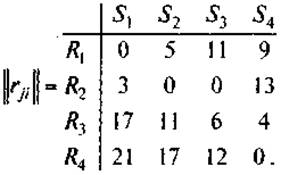
Полученные результаты вычислений с использованием критерия минимального риска Сэвиджа оформим в следующей таблице:
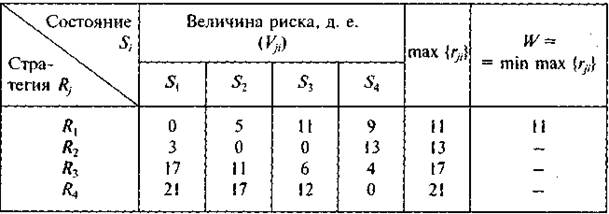
Введение величины риска rji, привело к выбору первой стратегии R1, обеспечивающей наименьшие потери (затраты) в самой неблагоприятной ситуации (когда риск максимален).
Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе стратегии, а значит, избежать большего проигрыша (потерь).
4.Критерий Гурвица.
Критерий Гурвицаоснован на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью (1 — α) и в самом выгодном состоянии с вероятностью α, где α — коэффициент доверия. Если результат Vji — прибыль, полезность, доход и т. п., то критерий Гурвица записывается так:

j i i
 Когда Vji представляет затраты (потери), то выбирают действие, дающее
Когда Vji представляет затраты (потери), то выбирают действие, дающее
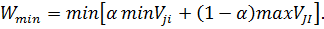
j i i
Если α = 0, получим пессимистический критерий Вальда.
Если α = 1, то приходим к решающему правилу вида max max Vji, или к так называемой стратегии «здорового оптимиста», т. е. критерий слишком оптимистичный.
Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов поведения соответствующими весами (1 — α) и α, где 0≤α≤1. Значение α от 0 до 1 может определяться в зависимости от склонности лица, принимающего решение, к пессимизму или к оптимизму. При отсутствии ярко выраженной склонности α = 0,5 представляется наиболее разумной.
Пример 7. Критерий Гурвица используем в примере 4. Положим α = 0,5. Результаты необходимых вычислений приведены ниже:
| Wj | min Vji i | max Vji i | 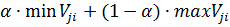 i i
i i
| min Wj j |
| W1 | ||||
| W2 | 17,5 | - | ||
| W3 | - | |||
| W4 | - |
Оптимальное решение заключается в выборе W.
Таким образом, в примере предстоит сделать выбор, какое из возможных решений предпочтительнее:
по критерию Лапласа — выбор стратегии R2,
по критерию Вальда — выбор стратегии R3;
по критерию Сэвиджа — выбор стратегии R1;
по критерию Гурвица при α = 0,5 — выбор стратегии R1, а если лицо, принимающее решение, — пессимист (α = 0), то выбор стратегии R3.
Это определяется выбором соответствующего критерия (Лапласа, Вальда, Сэвиджа или Гурвица).
Выбор критерия принятия решений в условиях неопределенности является наиболее сложным и ответственным этапом в исследовании операций. При этом не существует каких-либо общих советов или рекомендаций. Выбор критерия должно производить лицо, принимающее решение (ЛПР), с учетом конкретной специфики решаемой задачи и в соответствии со своими целями, а также опираясь на прошлый опыт и собственную интуицию.
В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем и ЛПР намерено вложить в некоторое предприятие столько средств, чтобы потом оно не сожалело, что вложено слишком мало, то выбирают критерий Сэвиджа.
Задание для самостоятельного решения: написать программу на языке С++ для выбора наиболее эффективного проекта легкового автомобиля для производства, используя критерии Лапласа, Вальда, Сэвиджа и Гурвица.
Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля

Определена экономическая эффективность Vji каждого проекта в зависимости от рентабельности производства. По истечению трех сроков  рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д.е.):
рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д.е.):
| Проекты | Состояния природы | ||
| S1 | S2 | S3 | |
| R1 | |||
| R2 | |||
| R3 | |||
| R |
Требуется выбрать лучший проект для производства, используя критерии Лапласа, Вальда, Сэвиджа и Гурвица при ɑ=0,1. Сравните решения и сделайте выводы.
Date: 2015-08-15; view: 2200; Нарушение авторских прав