Понятие корреляционного и регрессионного анализа

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, эти данные являются значениями случайной величины.

Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).

Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.

Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена.

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от лат. correlatio соотношение, соответствие). Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) показателями (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов.

Характер связи между показателями определяется по корреляционному полю. Если y зависимый признак, а x независимый, то, отметив каждый случай x (i) с координатами x _i и y _i , получим корреляционное поле. По расположению точек можно судить о характере связи (рис. 2.1).

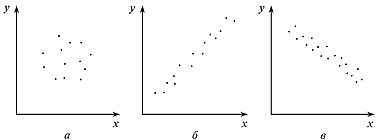
Рисунок 1 – Примеры корреляционных полей:

а переменные x и y не коррелируют; б наблюдается сильная положительная корреляция; в наблюдается слабая отрицательная корреляция

Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы. Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от - 0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.

Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна.

Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются:

а) на линейные:

y=a+bx,

где x экзогенная (независимая) переменная, y эндогенная (зависимая, результативная) переменная, a, b параметры;

б) степенные: y=a^.x^b

в) показательные: y=a^.b^x

г) прочие.

Date: 2015-08-15; view: 684; Нарушение авторских прав