
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение параметров линейного однофакторного уравнения регрессии
|
|
Пусть у нас имеются данные о доходах (x) и спросе на некоторый товар (y) за ряд лет (n):
| Год i | Доход x | Спрос y |
| x 1 | y 1 | |
| x 2 | y 2 | |
| x 3 | y 3 | |
| ... | ... | ... |
| n | x n | y n |
Предположим, что между x и y существует линейная взаимосвязь, т.е. y=a+bx.
Для того, чтобы найти уравнение регрессии, прежде всего нужно исследовать тесноту связи между случайными величинами x и y, т.е. корреляционную зависимость.
Пусть
x 1 , x 2 ,..., x n совокупность значений независимого, факторного признака;
y 1 , y 2 ,..., y n совокупность соответствующих значений зависимого, результативного признака;
n количество наблюдений.
Для нахождения уравнения регрессии вычисляются следующие величины:
1. Средние значения
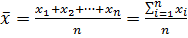 для экзогенной переменной;
для экзогенной переменной;
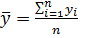 для эндогенной переменной.
для эндогенной переменной.
2. Отклонения от средних величин
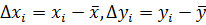
3. Величины дисперсии и среднего квадратичного отклонения
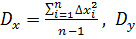 =
=  ;
;
 .
.
Величины дисперсии и среднего квадратичного отклонения характеризуют разброс наблюдаемых значений вокруг среднего значения. Чем больше дисперсия, тем больше разброс.
4. Вычисление корреляционного момента (коэффициента ковариации):
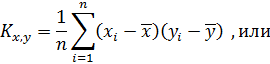
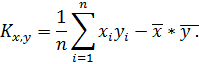
Корреляционный момент отражает характер взаимосвязи между x и y. Если K x, y > 0, то взаимосвязь прямая. Если K x, y < 0, то взаимосвязь обратная.
5. Коэффициент корреляции вычисляется по формуле
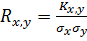 .
.
Доказано, что коэффициент корреляции находится в интервале от минус единицы до плюс единицы (- 1 >= R x, y <= 1). Коэффициент корреляции в квадрате 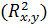 называется коэффициентом детерминации.
называется коэффициентом детерминации.
Если R x, y > |0,8|, то вычисления продолжаются.
6. Вычисления параметров регрессионного уравнения.
Коэффициент b находится по формуле

После чего можно легко найти параметр a:
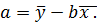
Коэффициенты a и b находятся методом наименьших квадратов, основная идея которого состоит в том, что за меру суммарной погрешности принимается сумма квадратов разностей (остатков) между фактическими значениями результативного признака y i и его расчетными значениями y i р , полученными при помощи уравнения регрессии
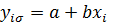 .
.
При этом величины остатков находятся по формуле
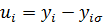 ,
,
где y i фактическое значение y; y i σ расчетное значение.
Пример 1: Линейная регрессия, нахождение уравнения регрессии.
Задание: С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты X и числа уволившихся за год рабочих Y, данные приведены в таблице 2:
Таблица 1- соотношение зарплаты и кол-ва уволившихся рабочих
| X | |||||
| Y |
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.
Решение: Сначала найдем характеристики случайных величин X и Y (выборочное среднее и выборочное среднее квадратичное отклонение).
Таблица 2 – вычисление выборочного среднего и выборочного среднего квадратичного отклонения для X
Сумма
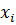
| ||||||
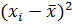
|
Выборочная средняя 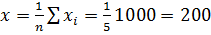
Выборочная дисперсия 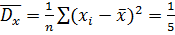 25000=500
25000=500
Выборочное квадратичное отклонение 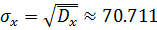
Таблица 3 – вычисление выборочного среднего и выборочного среднего квадратичного отклонения для Y
Сумма
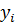
| ||||||
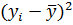
|
Выборочная средняя 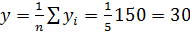
Выборочная дисперсия 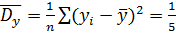 1350=270
1350=270
Выборочное квадратичное отклонение 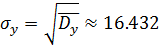
Осталось подсчитать 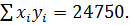 Подсчеты занесем в таблицу:
Подсчеты занесем в таблицу:
Таблица 4 - вычисление произведений xiyi и их суммы
| xi | ||||||
| yi | Сумма | |||||
| xiyi |
Коэффициент корреляции вычислим по формуле
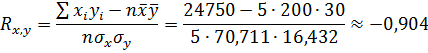
Уравнение регрессии Y на X имеет вид:
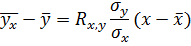
Подставляем все величины:
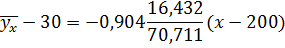
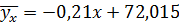
Пример 2: Линейная регрессия по корреляционной таблице, построение графика.
Задание: Найти выборочное уравнение прямой 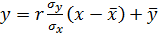 регрессии Y на X по заданной корреляционной таблицы.
регрессии Y на X по заданной корреляционной таблицы.
Таблица 5 - Корреляционная таблица
| Y/X | ny | ||||||
| nx | N=100 |
Решение: Построим ряды распределений для Y и X, вычислим их характеристики (выборочное среднее и выборочное среднее квадратичное отклонение)
Таблица 6 - Вычисление выборочного среднего и выборочного среднего квадратичного отклонения
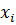
| 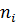
| 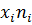
| 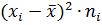
|
| 417,605 | |||
| 893,025 | |||
| 257,4325 | |||
| 15,125 | |||
| 677,655 | |||
| 333,9075 | |||
| Сумма | 259,75 |
Выборочная средняя 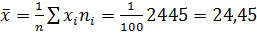
Выборочная дисперсия 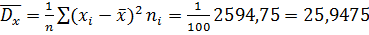
Выборочное квадратичное отклонение 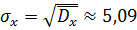
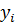
| 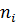
| 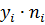
| 
|
| 4014,08 | |||
| 1230,08 | |||
| 1155,2 | |||
| 4336,64 | |||
| Сумма |
Выборочная средняя 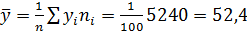
Выборочная дисперсия 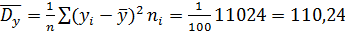
Выборочное квадратичное отклонение 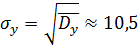
Коэффициент корреляции вычислим по формуле:

Найдем сумму 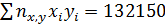
Тогда Rx,y= 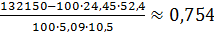
Уравнение регрессии Y на X имеет вид:
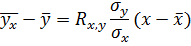
Подставляем все величины:
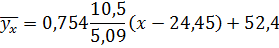

Построим корреляционное поле и линию регрессии:
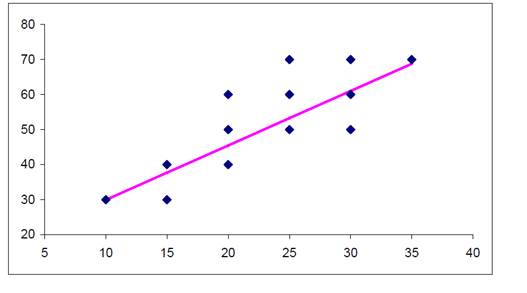
Рисунок 2- уравнение регрессии
Задание для самостоятельного решения: написать программу на языке С++ для нахождения уравнение регрессии и построения графика, отображающего корреляционное поле и линию регрессии.
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
Таблица 7- сведения об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| i | x | y |
Date: 2015-08-15; view: 1684; Нарушение авторских прав