Поверхности второго ряда

Поверхности второго порядка: сфера, эллипсоид, конус, гиперболоид, параболоид.

Сфера. Замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. S = 4π r ² , S = π d ².

Конус. Поверхность, образованная прямыми линиями, проходящими через данную точку Р и

пересекающими данную плоскую линию L (не проходящую через Р) называется

конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей.

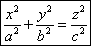- уравнение конуса

Эллипсоид. Поверхность, которая подходящим образом подобрана в системе координат и имеет уравнение

Эллипсоид – замкнутая овальная поверхность, где a, b, с – полуоси. Если все они различны, то эллипсоид называется трехосным. Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x²+y²+z²=R²

Гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

(однополостный гиперболоид), где a и b- действительные полуоси, а c - мнимая полуось;

или (двуполостный гиперболоид), где a и b- мнимые полуоси, а c - действительная полуось. При этом a, b и c - положительные числа. Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двуполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP − BP | = const. В этом случае A и B называются фокусами гиперболоида. Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

Параболоиды. Эллиптический. При пересечении поверхности координатами плоскостями Oxz и Oyz получается соответственно параболы 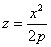и .

Таким образом, поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно

расширяющейся чаши.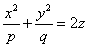

Date: 2015-08-15; view: 1010; Нарушение авторских прав