Функция натурального аргумента. Предел функции натурального аргумента

Функцию y = f(x), x Є N, называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или y₁, y₂, y₃, …, yn, … . Значения y₁, y₂, y₃ (и т.д.) называют соответственно первым, вторым, третьим (и т.д.) членами последовательности. В символе yn число n называют индексом, который задает порядковый номер того или иного члена последовательности.

Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n-го члена: yn = f(n).

Пример. yn = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Если существует такое число A, что для любого (сколь угодно малого) положительного числа ε найдется такое натуральное N (вообще говоря, зависящее от ε), что для всех n ≥ N будет выполнено неравенство |an – A| < ε, то говорят, что последовательность {an} сходится и A – ее предел.

Обозначается это так: .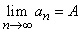

Геометрический смысл числовой последовательности. Неравенство ½an-a½ < e.равносильно двойному неравенству a - e < a n < a + e, что соответствует попаданию членов данной последовательности в e - окрестность точки а.

35. Определение предела функции в точке. Предел в функции при x →∞.

Записывать предел функции f(x) принято в виде , снизу указывается аргумент x и через стрелочку к какому значению x₀ он стремится.

Если x₀ представляет из себя конкретное действительное число, то говорят о пределе функции в точке.

Если x₀ = ∞ , x₀ = + ∞или x₀ = - ∞, то говорят о пределе функции на бесконечности.

Сам предел может быть равен конкретному действительному числу 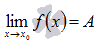, в этом случае говорят, что предел конечен.

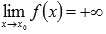Если , или 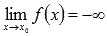, то говорят, что предел бесконечен.

Еще говорят, что предел не существует, если нельзя определить конкретное значение предела или его бесконечное значение (∞, + ∞или - ∞ ). Например, предел от синуса на бесконечности не существует.

предел функции на бесконечности.

Число А называется пределом функции f(x) при x →∞, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается .

Предел функции f(x) при x →∞ бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается .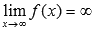

предела функции в точке.

Число В называется пределом функции f(x) слева при x →a, если для любой сходящейся к а последовательности аргументов функции x_n, значения которых остаются меньше а (x_n < a), последовательность значений этой функции сходится к В.

Обозначается .

Число В называется пределом функции f(x) справа при x →a, если для любой сходящейся к а последовательности аргументов функции , значения которых остаются больше а (x_n < a), последовательность значений этой функции сходится к В.

Обозначается .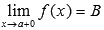

Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.

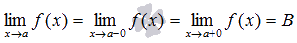
Предел функции f(x) в точке а бесконечен, если пределы слева и справа а бесконечны.